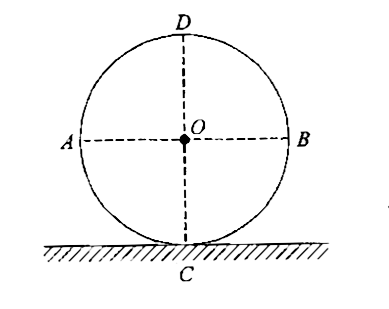
In a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass 2m. In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

The ring is now folded along the diameter AC, such that the plane of the section ABC is normal to the plane of the section ADC. (The angle BOD =90∘). It is then placed on a thin, fixed horizontal wire, ie.e, the diameter AC lies along the wire. The angle made by DO with the vertical will now be
tan−1(2/3)
tan−1(1/2)
30∘
60∘
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
In a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass 2m. In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

Let C1 denote the centre of mass of the section ABC and C2 denote the centre of mass of the section ADC. The distance C1C2 is equal toArB2r/3C2πr/5D4r/πIn a ring ABCD of radius r, the lower half ABC has mass m and the upper half ADC has mass 2m. In both parts, the masses are distributed evenly. The ring is initially at rest on a horizontal surface, as shown. O is the centre of the ring.

The ring is now pushed very slightly and begins to roll on the horizontal surface without slipping. When it has made half a rotation, i.e., B is vertically above D, its angualar velocity ω will be given by (where β=g/πr)Aω2=3β/2Bω2=4β/3Cω2=8β/5Dω2=9β/4Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionAn impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
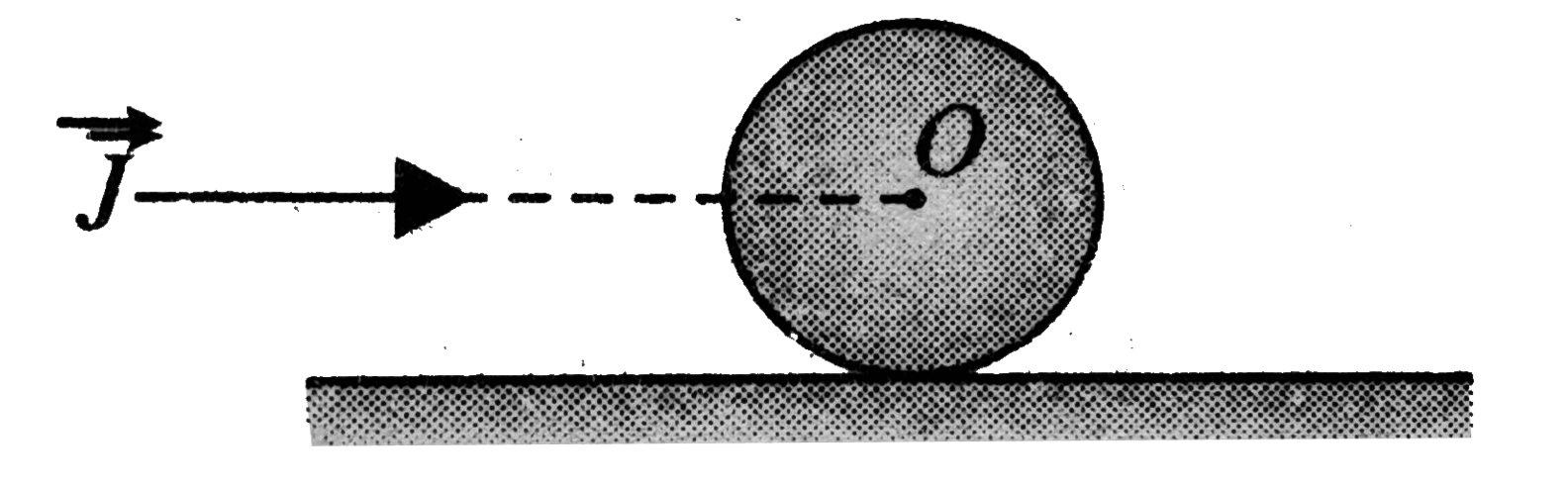
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
View SolutionAn impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is

View Solution
