Two long wires PQR and MNP carry equal current I as shown such that QR and NP are parallel. Find the magnetic field at origin O.

The correct Answer is:μ0I2√3πa out of the page
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Answer Type
37 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (integer)
1 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View Solution
Knowledge Check
Two long wires PQR and MNP carry equal current Ias shown such that QR and NP are parallel. Find the magnetic field at origin O.
 Aμ0I2√3πa into the pageBμ0I2πa out of the pageCμ0I2√3πa out of the pageDμ0I2πa into the page
Aμ0I2√3πa into the pageBμ0I2πa out of the pageCμ0I2√3πa out of the pageDμ0I2πa into the pageTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
A conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionTwo inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
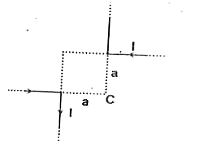
View Solution(a) Two long wires at a distance 2d apart carry equal, antiparallel current i. Find magnitude and direction of magnetic field at point A as shown.For what value of x, magnetic field is maximum? Also calculate maximum magnetic field. Sketch B versus x graph.

View SolutionA wire loop formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown in figure. Find the magnetic field induction at the centre O.

View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View Solution
