A system consists of charges +q and +q at the opposite corners of a square of sides 2a and −q and −q at the other two corners . Calculate the potential and field at a distance r from the centre of the square along a line parallel to the two sides of the square . Assume a <<r .
The correct Answer is:V=14πε0×3qa2r3,E=14πε0×9qa2r4
Step by step video, text & image solution for A system consists of charges +q and +q at the opposite corners of a square of sides 2a and -q and -q at the other two corners . Calculate the potential and field at a distance r from the centre of the square along a line parallel to the two sides of the square . Assume a lt lt r . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Four identical charges Q are fixed at the four corners of a square of side a. The electric field at a point P located symmetrically at a distance a/√2 from the center of the square is
AQ2√2πε0a2BQ√2πε0a2C2√2Qπε0a2D√2Qπε0a2 - Question 2 - Select One
A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
Aq=√2QBq=−√2QCq=2√2QDq=−2√2Q - Question 3 - Select One
The electric field at the centre of a square having equal charge q at each of the coner (side of square a )
A8kqa2B2kqa2CzeroD4kq(a/√2)2
Four point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
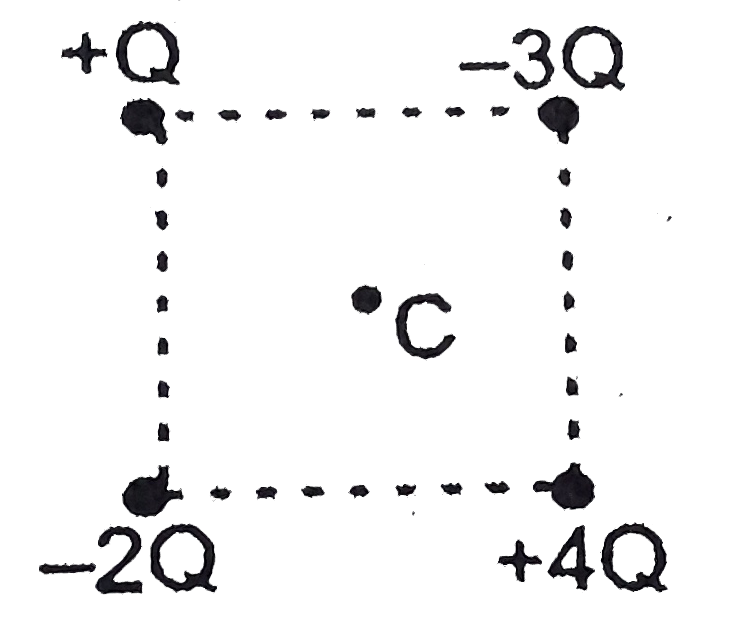 View Solution
View SolutionA system consists of two identical dipoles placed along the sides of a square ABCD in such a way that +q and +q lie at the corner A and C and −q and −q at the corner B . Calculate the potential due to the system on the diagonal BD at a distance r from the intersection of the diagonals of the square . The length of each diagonal is 2a .
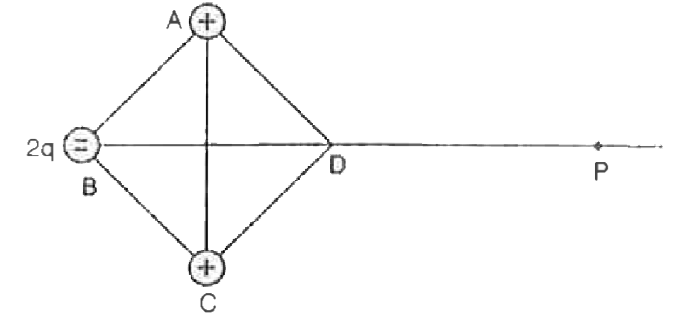 View Solution
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionA charge Q is placed at each of the opposite corners of square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero , then Q/q equals.
View SolutionA charge Q is place at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then Q/q equals:
View Solution


