Two identical dipoles have their axes at right angles to each other and also bisecting each other . Calculate the field at a distance r from the point of intersection of their axes in a direction θ with the axis of one of the dipoles . The dipole moment of each dipole is equal to p .
The correct Answer is:E=14πε0pr3√5+3sin2θ
Step by step video, text & image solution for Two identical dipoles have their axes at right angles to each other and also bisecting each other . Calculate the field at a distance r from the point of intersection of their axes in a direction theta with the axis of one of the dipoles . The dipole moment of each dipole is equal to p . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
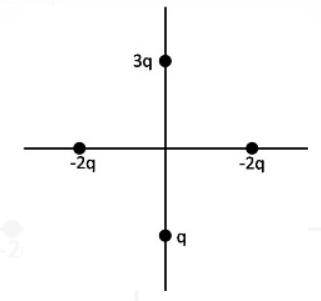
4 charges are placed each at a distance ‘a’ from origin. The dipole moment of configuration is
View SolutionTwo identical electric point dipoles have dipole moments −→P1=pˆiand−→P2=pˆi and are held on the x axis at distance 'a' from each other. When released, they move along the x-axis with the direaction of their dipole moments remaining unchanged. If the mass of each dipole is 'm', their speed when they are infinitely for apart is :
View Solution
Knowledge Check
The electric potential at a point on the axis of an electric dipole depends on the distance r of the point from the dipole as
A∝1rB∝1r2C∝rD∝1r3Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
AE∝1rBE∝1r4CE∝1r2DE∝1r3The electric potential V at a point on the axis of an electric dipole depends on the distance 'r of the point from the dipole as
AV∝1rBV∝1r2CV∝1r3DV∝r
Two magnetic dipoles of moments 0.108 and 0.122Am2 are placed along two lines drawn on the table at right angles to each other. Find the intensity at the point of intersection of their axes, their centres being 0.3 and 0.4m, respectively from the point of intersection.
View SolutionThe electric potential at a point distant 0.1m from the middle of a short electric dipole on a line inclined at an angle of 60∘ with the dipole axis is 900V. Calculate the dipole moment.
View SolutionElectric field intensity (E) due to an electric dipole varies with distance (r) from the point of the center of dipole as :
View SolutionAn electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View SolutionA tiny electric dipole of dipole moment p is palced at a distance r from an infinitely long wire, with its →p normal to the wire. If the linear charge density of the wire is λ, the electrostatic force acting on the dipole is equal to
View Solution
