A mass M attached to the end of a small flexible rope of diameter d=1 cm is raised vertically by winding the rope on a reel. If the reel is turned uniformly ay the rate of n=2 rps, what will be the tension T in the rope? Neglect inertia of the rope and slight lateral motion of the suspended mass. (Fig.5.25)

The correct Answer is:T=Mg(1+2πn2dg)=1.025Mg
Topper's Solved these Questions
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (A)
27 Videos
- KINETIC THEORY OF GASESBOOK - NN GHOSHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
24 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
Similar Questions
A rope of length of 2m is tied between two ends . If the speed of transverse waves propagating in the rope is 4ms−1 and the tension in the rope is 2 N , find the mass of the rope is C.G.S units .
View SolutionOne end of a 60m long rope of mass 1.8 kg is tied to a rigid horizontal support held high above the ground. The rope hangs vertically and kept taut by a weight 'W' suspended at its lower end. A person jerks the lower end of the rope sideways in a sinusoidal manner and a transverse wave of frequency 2 Hz and amplitude 10cm passes along the rope such that there are 2 cycles of the wave in the total length of the rope. Neglecting the weight of the rope as compared to the suspended weight W and with g = 10m/s2, answer the following questions. (S=75×10−4m2)

In the questions above, weight of the rope has been neglected as compared to the suspended weight. However, if we also account for the weight of the rope. the speed of the wave at the top of the rope will be
View Solution
Knowledge Check
A mass 1kg attached to the end of a flexible rope of diameter d=0.25mis raised vertically by winding the rope on a reel as shown. If the reel is turned uniformly at the rate of 2r.p.s. What is the tension in rope. The inertia of rope may be neglected.
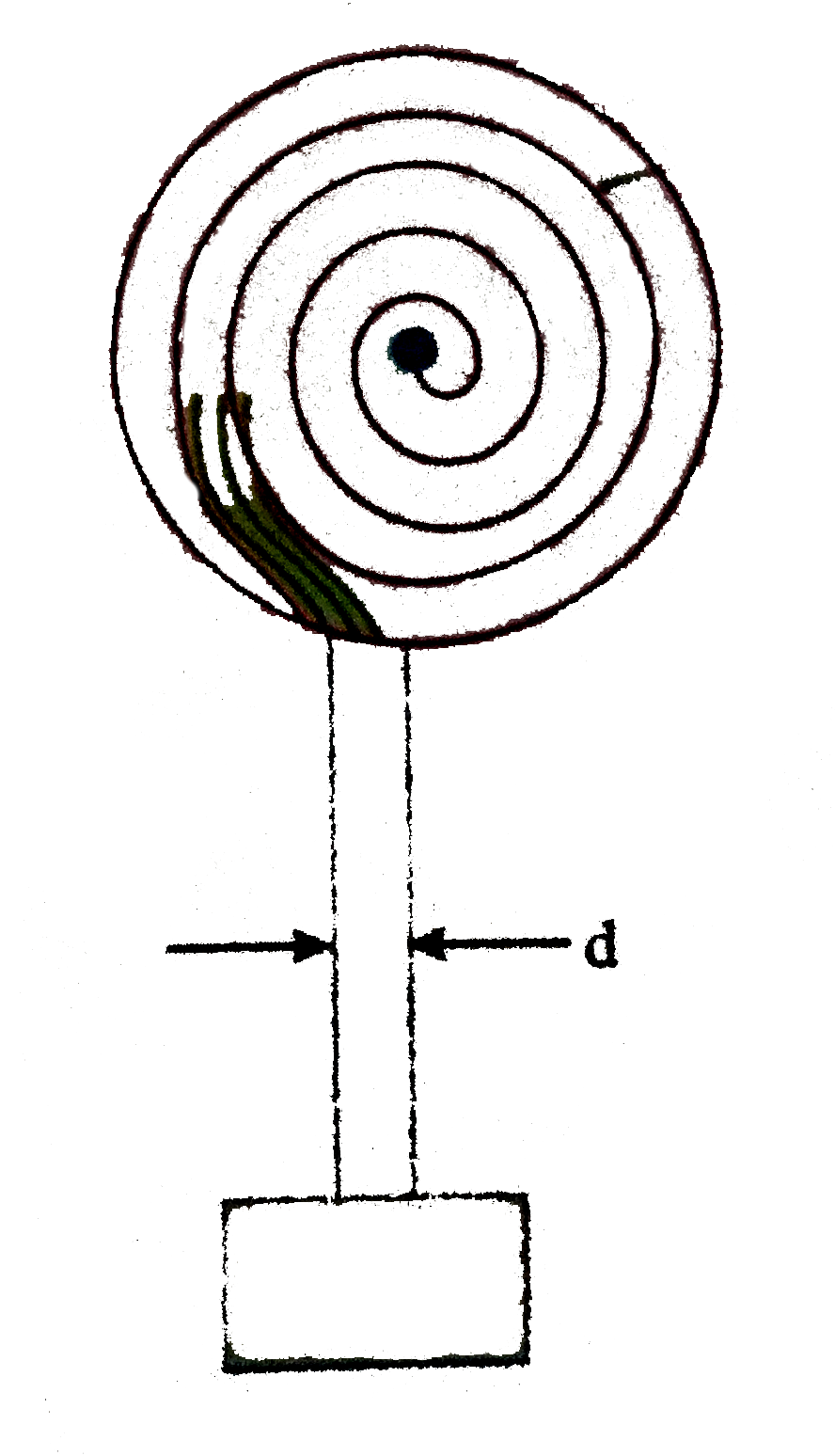 A16.28NB10NC20ND1N
A16.28NB10NC20ND1NAn object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 NA rope of mass 5 kg is moving vertically in vertical position with an upwards force of 100 N acting at the upper end and a downwards force of 70 N acting at the lower end. The tension at midpoint of the rope is
A100 NB85 NC75 ND105 N
A rope, with mass 1.39 kg and fixed at both ends oscillates in a second-harmonic standing wave pattern. The displacement of the rope is given by
y−(0.10m)(sinπx/2)sin12πt.
where x=0 at one end of the rope, x is in meters and t is in seconds. What are (a) the length of the rope, (b) the speed of the waves on the rope, and (c) the tension of the rope? (d) If the rope oscillates in a third-harmonic standing wave pattern, what will be the period of oscillation?
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40 N in the horizonal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling? (Neglect the mass of the rope, g=10m/s2)
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceilling A force of 40N in the horizontal direction is applied atmidpoint P of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, g=10m/s2) .
View SolutionSee Fig 5.8 .A mass of 6 kg is suspended by a rope of length 2m from the ceiling . A force of 50 N in the horizontal direction is applied at the mid-point P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium ? (Take g = 10 m s−2). Neglect the mass of the rope.
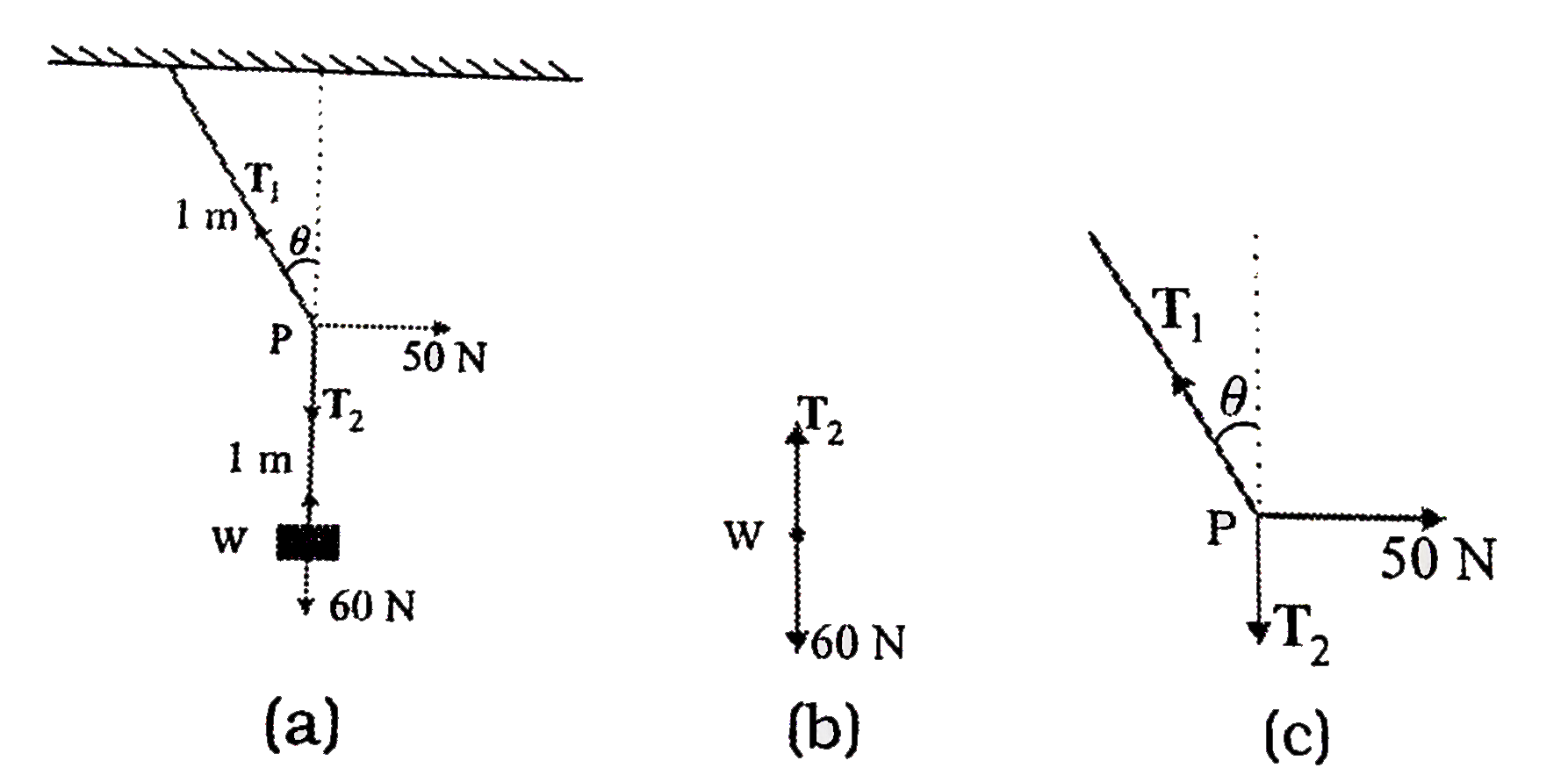
View SolutionA mass of 10 kg is suspended vertically by a rope of length 2 m from a ceiling. A force of 60 N is applied at the middle point of the rope in the horizontal direction, as shown in Fig. Calculate the angle the rope makes with the vertical. Neglect the mass of the rope and take g=10ms−2.

View Solution
