What is the maximum offset that can obtain by piling up four identical bricks of length l ?
[Hints :CG if any two from top must pass through the edge of the third beneath . The uppermost brick may overhang by 12 .]
The correct Answer is:1112l
Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
Similar Questions
Suppose you have to pile up uniform bricks to erect an inclined wall by offsetting each brick by a constant fraction ,1n , of a brick length l over the beneath. How many bricks can be piled by before the wall collapse ? How high a wall can erect if the size of each bricks is 7.5cm×12.5cm×25cm and the offset is only 110 of the length of each bricks? What is the total offset you get ?
[Hints: The vertical line through CG of the wall must pass through the base. The moment it goes beyond the base brick, the wall will collapse.]
View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
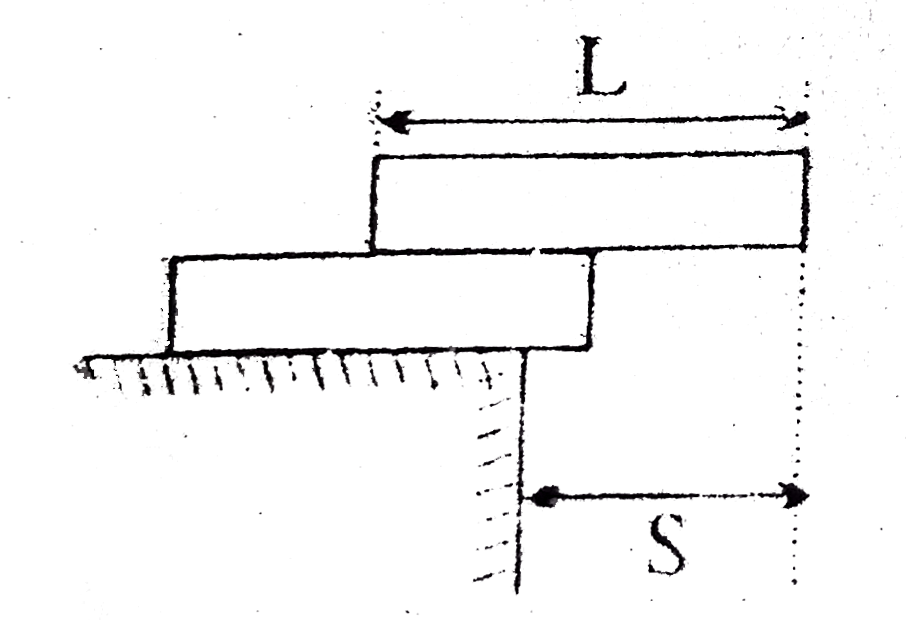
View Solution
Knowledge Check
What is the maximum off set that one can obtained by piling up three identical bricks of length l :
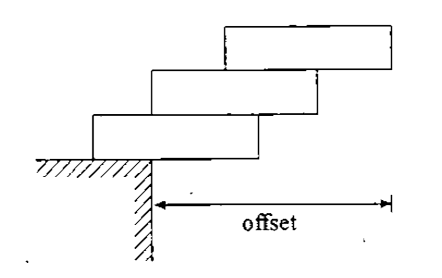A23lB43lC56lD1112lTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
A12LB23LC34LD78LABCD is a square of side length 2. C1 is a circle inscribed in the square and C2 is a circle. circumscribing the square. P and Q are any two points on C1andC2 respectively. Also R is fixed point and L is a fixed line in the same plane. A circle C touches line L and circle C1 externally. S is a point which is equidistant from given point Rand fixed line L. Point R coincides with B.
Line Lpasses through A and Cand a line parallel to AC passes through B. If the locus of S cuts this line at 2 points T1 and T2 and the diagonal BD at T3, the area of triangle T1T2T3 is :A1 sq. unitB12 sq. unitC2 sq. unitsD3 sq. units
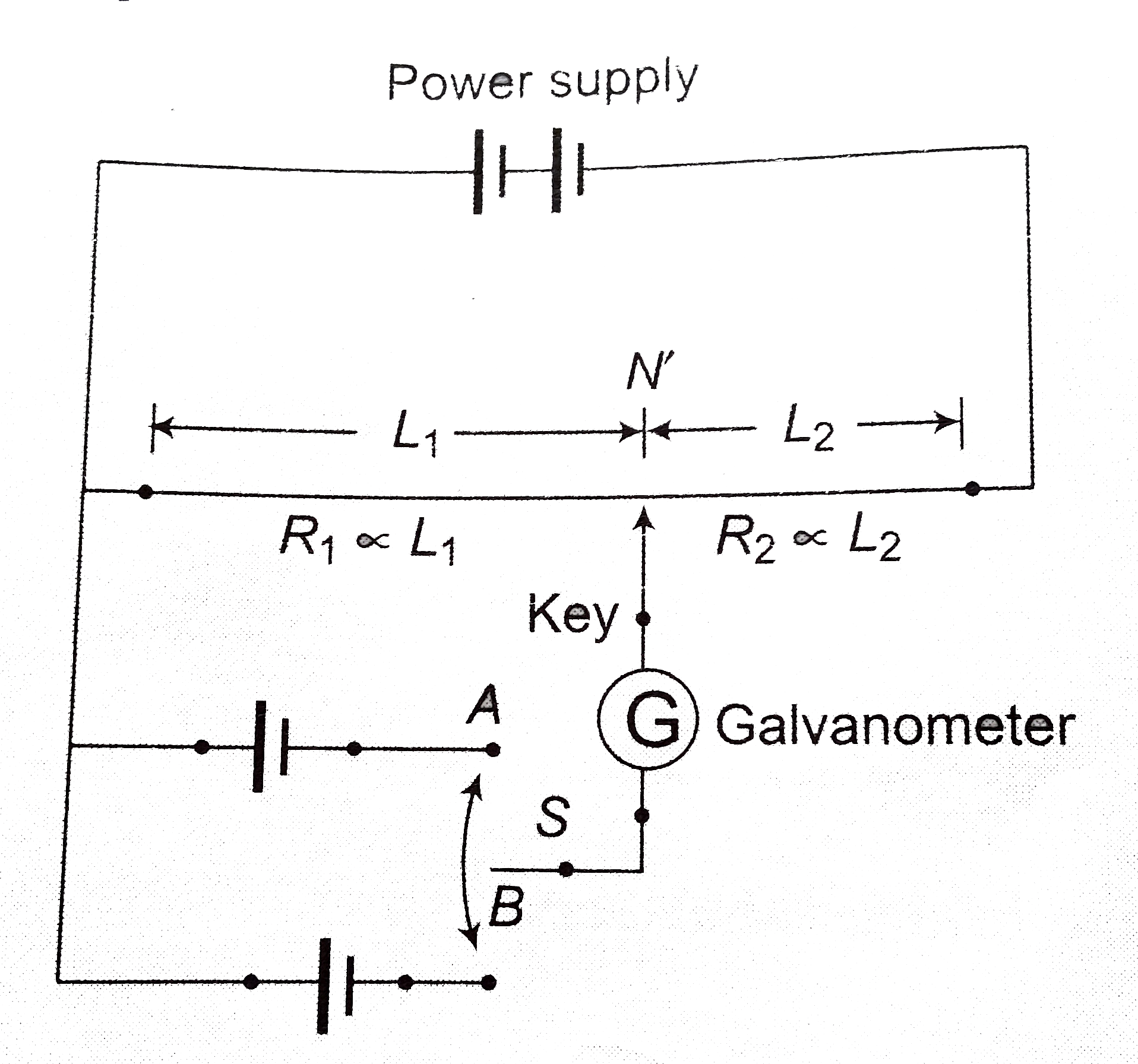
A slide-wire potentiometer is shown in the figure. In this device the resistances R1 and R2 of figure are actually a uniform wire 1.000m in length. Hence, the resistance R1 is alphaortional to length L1 and the resistance R2 is alphaortional to the length L2. the galvanometer junction N' in the figure is sharp-edged key that can slide along the wire and be made to make contact with ot at any position along its length. When a standard cell with an emf of 1.6V is used and the switch S is in position A, the length L1 is 40cm for no current to flow through the galvanometer. When the switch is moved to position B, the length L1 must be changed to 60cm for tge galvanometer to carry no current. What is the value of the emf E2 ?
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular peth which lies in a horizantal plane. The length of the stribng from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
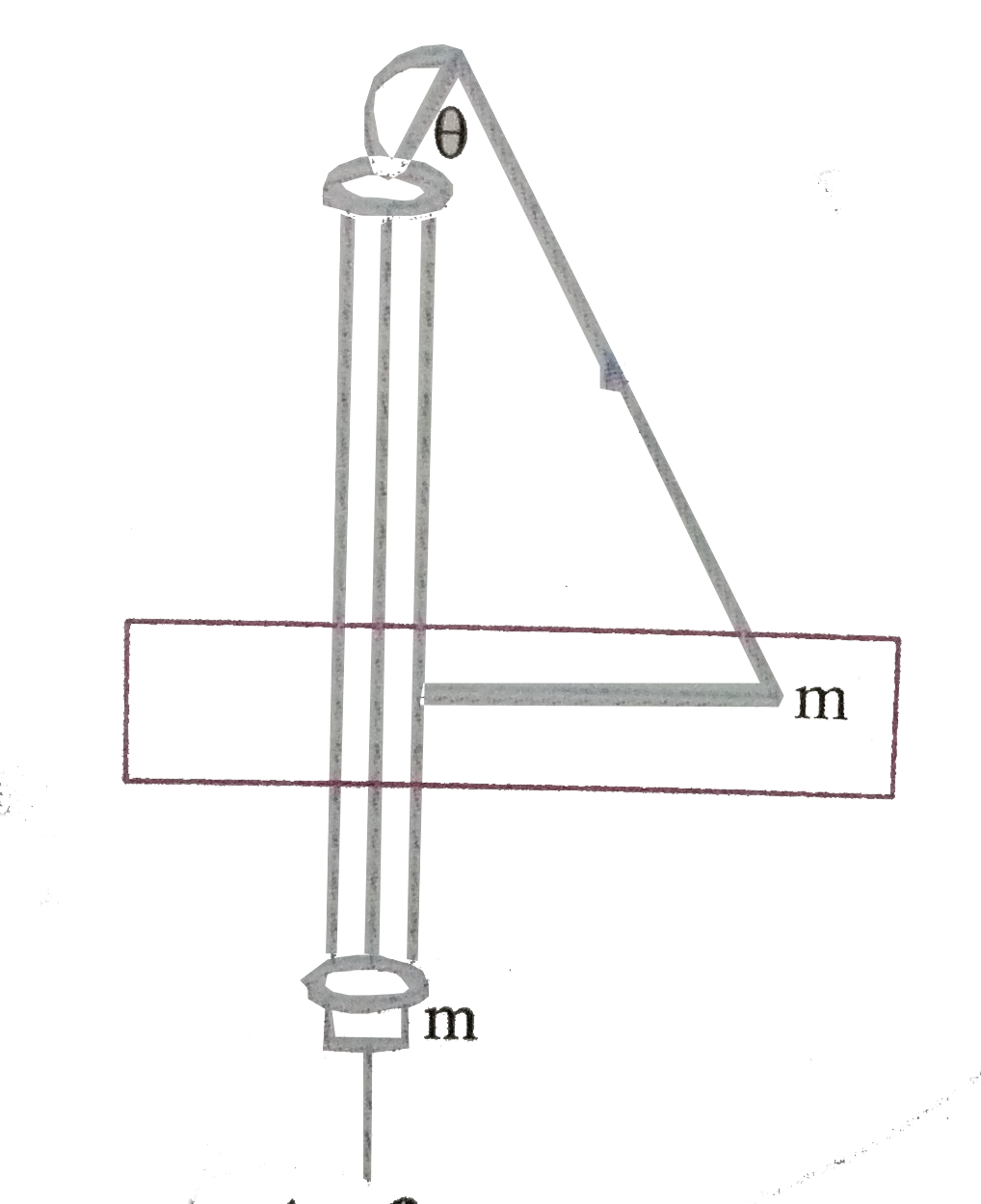
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
View SolutionA weightless rod of length 2l carries two equal masses 'm' , one secured at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing through C. What horizontal velocity must be imparted to the mass at A so that it just completes the vertical circle.
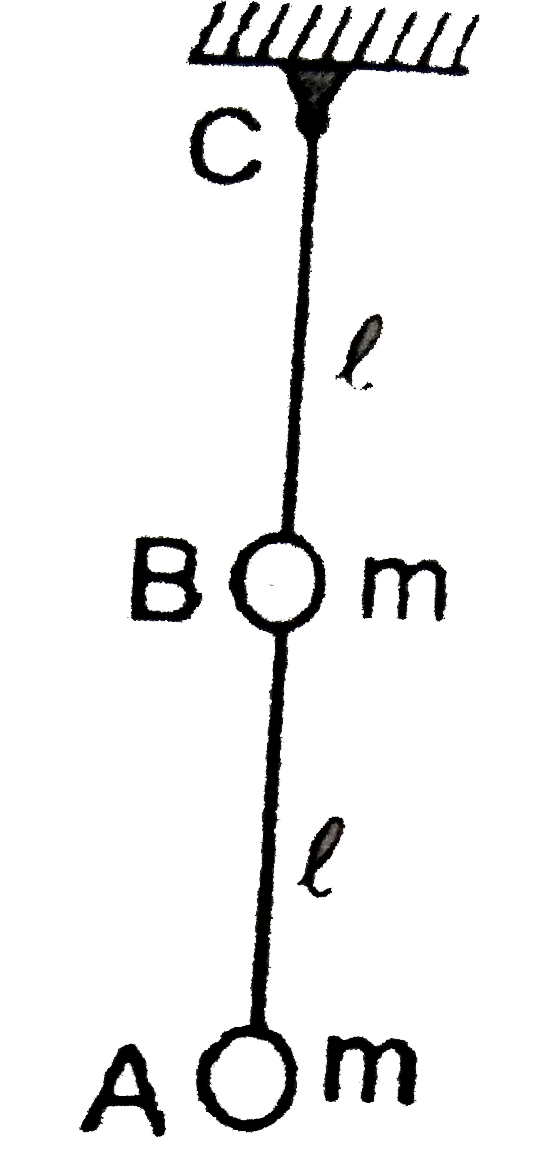
View SolutionSumati wanted to see the stars of the night sky. She knows that she needs a telescope to see those distant stars. She finds out that the telescopes, which are made of lenses, are called refracting telescopes and the ones which are made of mirrors are called reflecting telescopes.
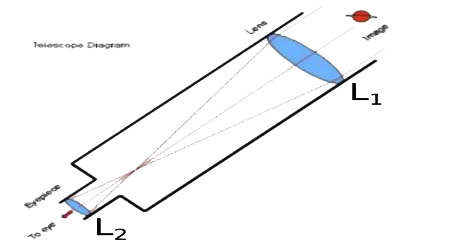
So she decided to make a refracting telescope. She bought two lenses, L1 and L2. out of which L1 was bigger and L2 was smaller. The larger lens gathers and bends the light, while the smaller lens magnifies the image. Big, thick lenses are more powerful. So to see far away, she needed a big powerful lens.Unfortunately, she realized that a big lens is very heavy. Heavy lenses are hard to make and difficult to hold in the right place. Also since the light is passing through the lens, the surface of the lens has to be extremely smooth. Any flaws in the lens will change the image. It would be like looking through a dirty window.
If the powers of the lenses L1 and L2 are in the ratio of 4:1, what would be the ratio of the focal length of L1 and L2
View Solution