A thin horizontal bar AB of negligible mass and length l is hinged to a vertical wall at A and supported at B by thin wire BC which is tied to a point C vertically above in the same wall.BC makes angle θ with the horizontal . A weight W is moved along the bar. Show how the tensile force T in the thin wire changes with the distance x of the weight from the wall.
The correct Answer is:Wx/lsinθ
Step by step video, text & image solution for A thin horizontal bar AB of negligible mass and length l is hinged to a vertical wall at A and supported at B by thin wire BC which is tied to a point C vertically above in the same wall.BC makes angle theta with the horizontal . A weight W is moved along the bar. Show how the tensile force T in the thin wire changes with the distance x of the weight from the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
Similar Questions
In figure a thin horizontal bar AB of negligible weight and length L is pinned to a vertical wall at A and supported at B by a thin wire BC that makes an angle θ with the horizontal. A weight W can be moved anywhere along the bar; its position is defined by the distance x from the wall of its centre of mass. As a function of x, the horizontal component of the reaction at the hinge A is?
View SolutionOne end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight αW is attached at the point Q at a height L above the hinge at point O. A block of weight αW is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(√2)W. Which of the following statements is/are correct?
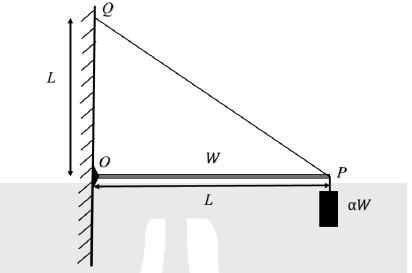
View Solution
Knowledge Check
Two projectiles A and B are thrown with the same speed such that A makes angle θ with the horizontal and B makes angle θ with the vertical, then -
ABoth must have same time of flightBBoth must achieve same maximum heightCA must have more horizontal range than BDBoth may have same time of flightA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
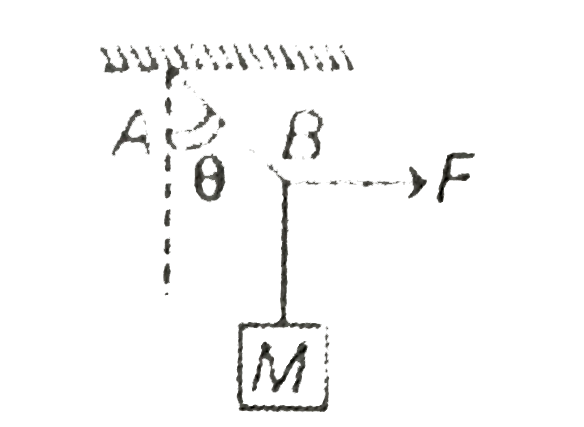AF sinθBF/sinθCFcosθDF/cosθA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
A√2glB√3glC√5glD√mgl
A point A on a sphere of weight w rests in contact with a smooth vertical wall and is supported by a string joining a point B on the sphere to a point C on the wall. Draw free body diagrame of the spheres.
View SolutionA uniform horizontal beam of length L and mass M is attached to a wall by a pin connection. Its far end is supported by a cable that makes an angle θ with the horizontal . If a man of mass 'm' stands at a distance l from the wall , find the tension in the cable in equilibrium.
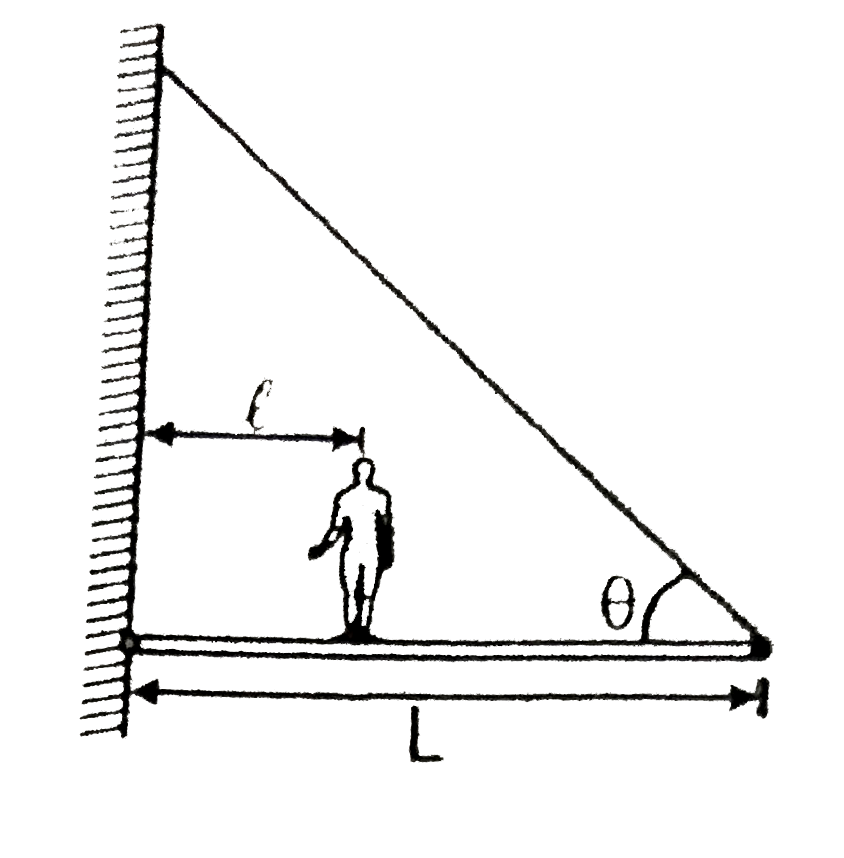
View SolutionA heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
View SolutionA ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
View SolutionThe x−t graph of particle moving along a straight line is shown in figure
Two projectiles A and b are thrown will the same speed such that A makes anle θ with the horizontal and B makes angle θ with the vertical, then
View Solution