Consider the system of weights P1=1kg,P2=2kg,P3=5kgandP4=0.5kg as shown in Figure 7.14. α=30∘,g=9.8ms−2 and the coefficient of friction between the weights and the planes is 0.2 Find (a) the acceleration of the system (b) tensions in the strings between P1andP2 and that between P2andP2 respectively and (c) the force with which P4 presses down on P3
![Consider the system of weights P(1)=1 kg,P(2) = 2 kg,P(3) = 5kg and P(4) = 0.5 kg as shown in Figure 7.14. alpha = 30^(@), g = 9.8 ms^(-2) and the coefficient of friction between the weights and the planes is 0.2 Find (a) the acceleration of the system (b) tensions in the strings between P(1) and P(2) and that between P(2) and P(2) respectively and (c) the force with which P(4) presses down on P(3) [Hint : Make free-body diagrams and apply Newton's law of motion after resolving the forces acting on a body along and perpendicular to the plane on which it lies]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NEP_NGM_PHY_GP_C07_E01_029_Q01.png)
[Hint : Make free-body diagrams and apply Newton's law of motion after resolving the forces acting on a body along and perpendicular to the plane on which it lies]
The correct Answer is:6.87ms−2 (b) 8.83N,16.12N (c) 1.465 N
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (A)15videos
FRICTION, WORK POWER AND ENERGY
- BOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions39videos
FIRST LAW OF THERMODYNAMICS
- BOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE29videos
GRAVITATION
Similar Questions
In the adjacent figure, masses of A,B and C are 1kg,3kg and 2kg respectively. Find
(a) the acceleration of the system and
(b) tension in the strings.
Neglect friction.(g=10m/s2)
View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find
(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View Solution
Knowledge Check
- Question 1 - Select One
What is the relationship between P1 and P2AGeometrical isomersBOptical isormersCPositional isomersDChain isomers - Question 2 - Select One
A block of mass m = 1 kg is placed over a plank Q of mass M = 6 kg, placed over a smooth horizontal surface as shown in figure. Block P is given a velocity v=2m/s2 to the right. If the coefficient of friction between P and Q is μ=0.3. Find the acceleration of Q relative to P.
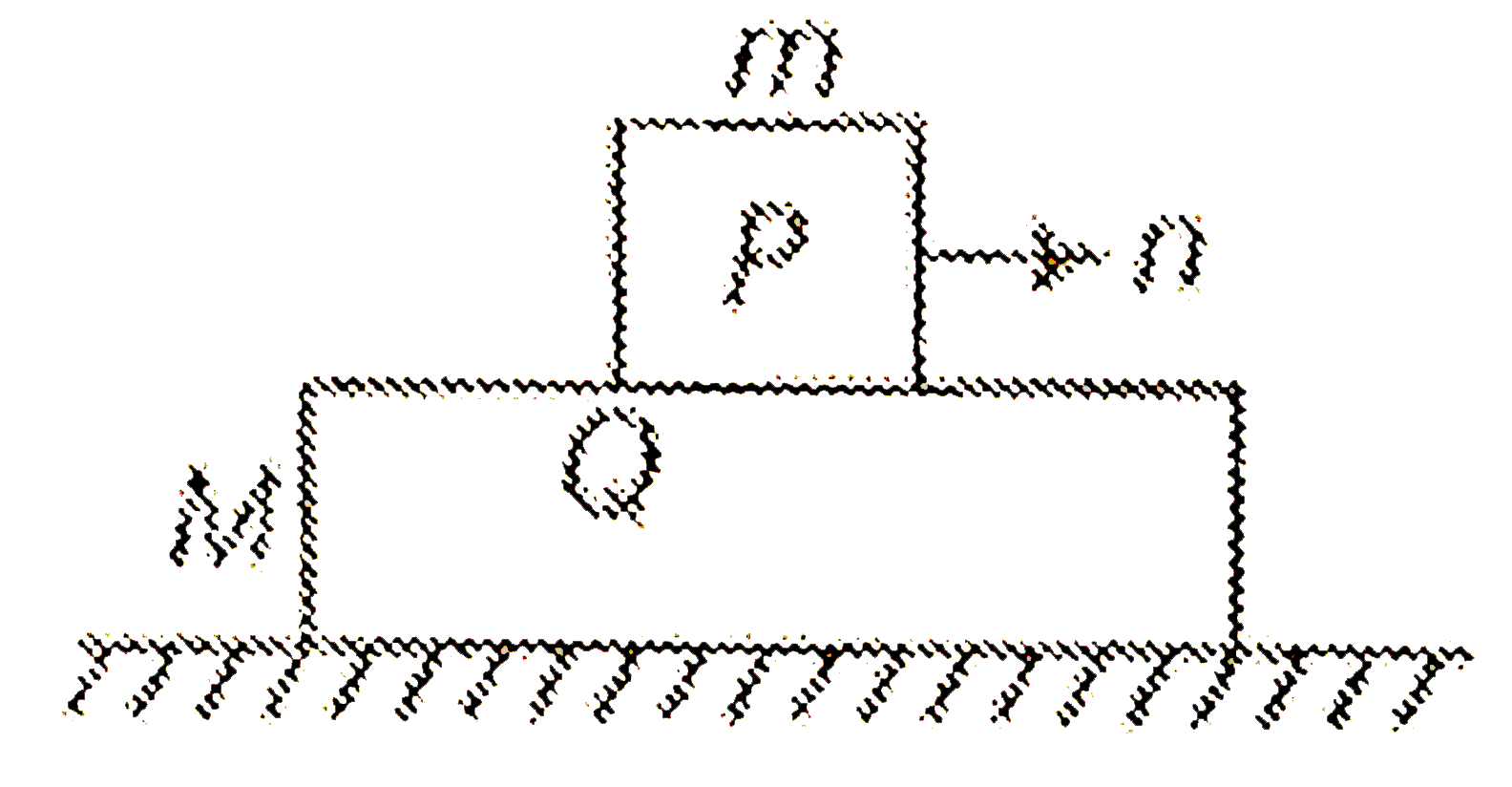A4m/s2B3.5m/s2C2m/s2D10.0m/s2 - Question 3 - Select One
P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
The angle between P1andP2 is ________.Acos−1(15)Bcos−1(1√55)Ccos−1(2√11)Dcos−1(3√11)
In the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find
(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find
(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionIn the adjacent figure, mass of A, B and C are 1 kg , 3 kg and 2 kg, respectively. Find
(a) the acceleration of the system, and
(b) tensions in the string .
Neglect friction. (g=10ms−2)View SolutionIn the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .
View SolutionIn the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.
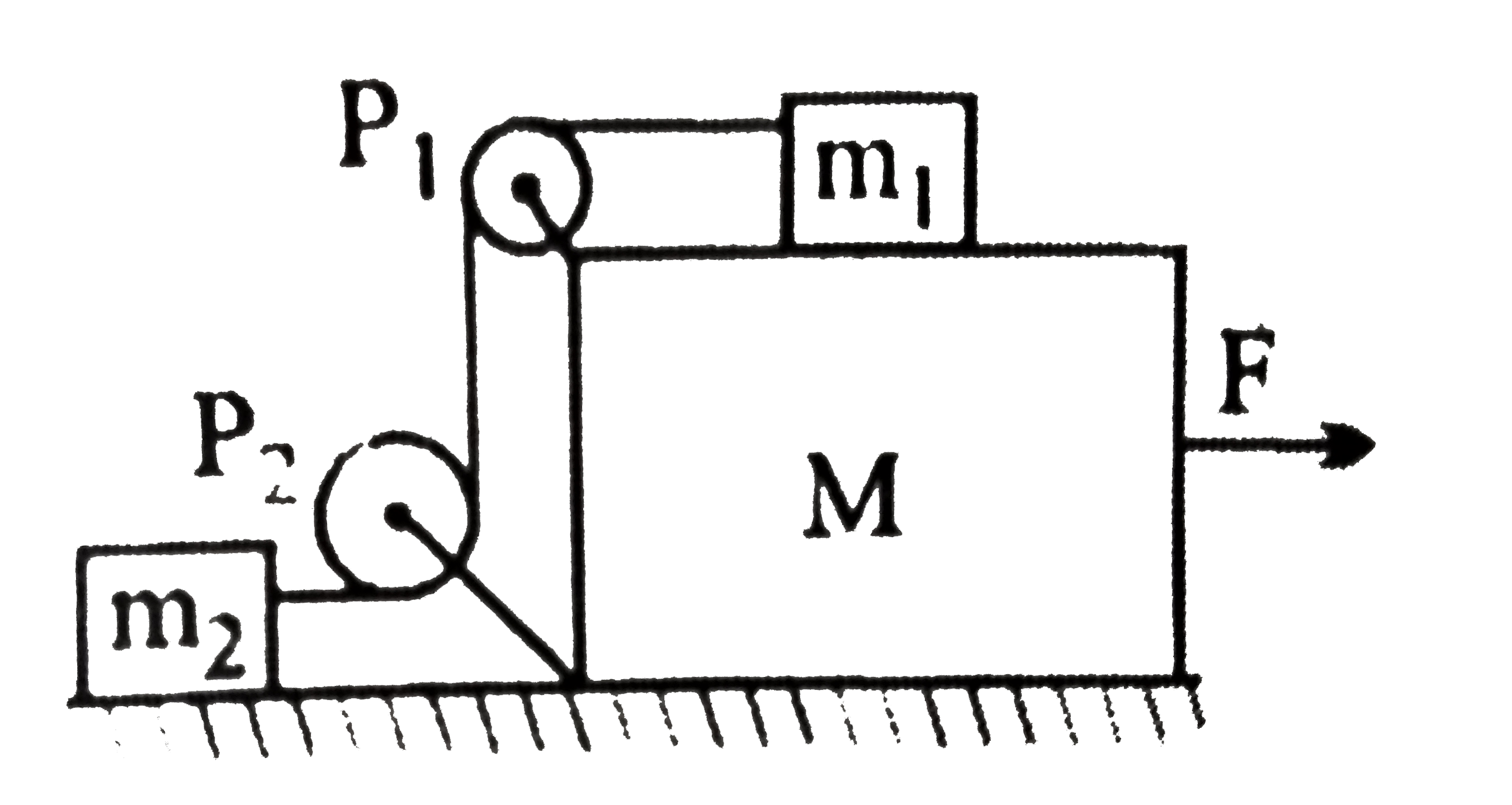
(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.View Solution