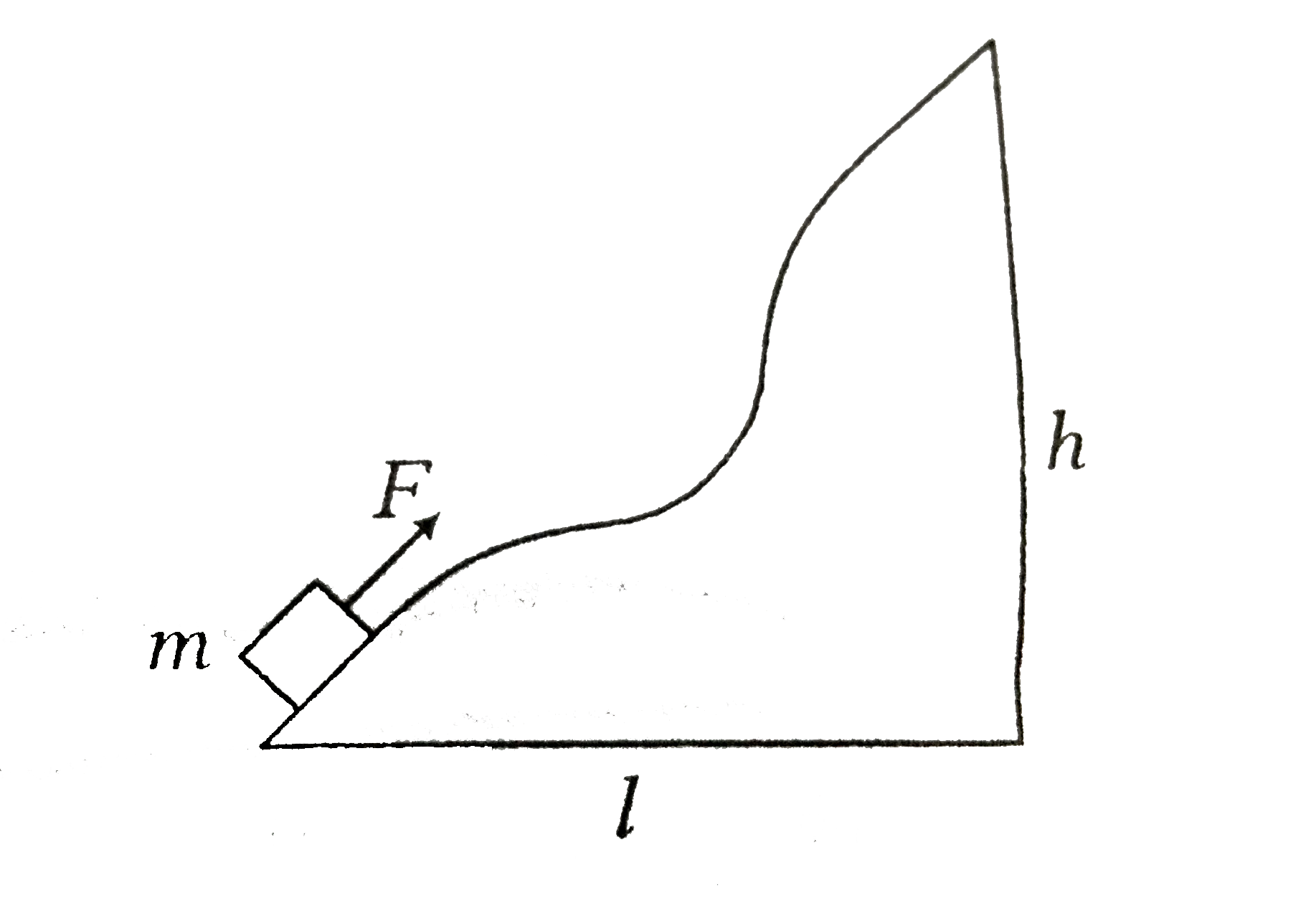
A body of mass m was slowly hauled up the hill as shown in the fig. by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base is I and the coefficient ot friction is μ.
 .
.
The correct Answer is:W=mg(h+μl)
Step by step video, text & image solution for A body of mass m was slowly hauled up the hill as shown in the fig. by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base is I and the coefficient ot friction is mu. . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (A)15videos
FRICTION, WORK POWER AND ENERGY
- BOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions39videos
FIRST LAW OF THERMODYNAMICS
- BOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE29videos
GRAVITATION
Similar Questions
A body of mass m was slowly hauled up the hill (figure) by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base l, and the coefficient of friction k.
 View Solution
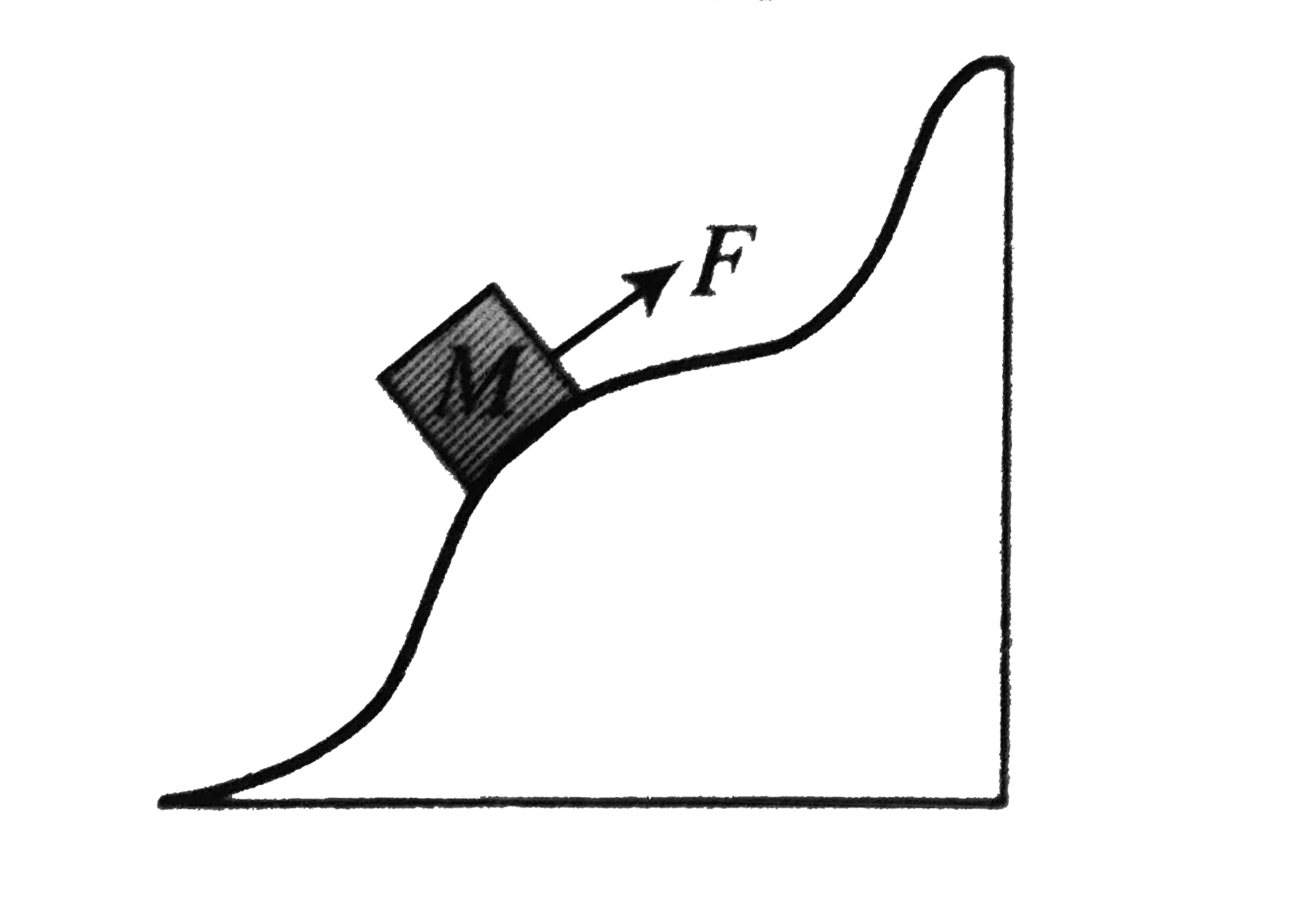
View SolutionA body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces are smooth. Find the work done by this force
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces aresmooth. Find the work performed by this force.
 AmglB−mglCmghDzero
AmglB−mglCmghDzero - Question 2 - Select One or More
A body of mass M was slowly hauled up a rough hill by a force F which at each point was directed along a tangent to the hill. Work done by the force
 A(a) Is independent of the shape of trajectoryB(b) Depends upon the vertical component of displacement but is independent of horizontal componentC(c) Depends upon both the componentsD(d) Does not depend upon the coefficient of friction
A(a) Is independent of the shape of trajectoryB(b) Depends upon the vertical component of displacement but is independent of horizontal componentC(c) Depends upon both the componentsD(d) Does not depend upon the coefficient of friction - Question 3 - Select One
A small block of mass m os takes slowly up a fixed hemisphere from P to Q and then slowly down along its surface from Q to S by force F, which at each point of the surface, is tangential to the surface. If the coefficient of friction is μ, then the work performed by the force F in taking the block from P to S along the hemispherical surface of radius R is :
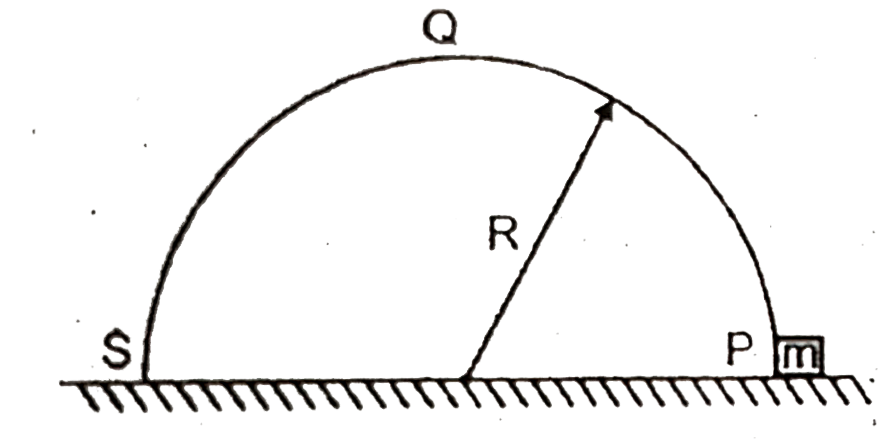 A2μmgRBμmgRCπμmgRDNone of these
A2μmgRBμmgRCπμmgRDNone of these
A body of mass m was slowly hauled up the hill (figure) by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base l, and the coefficient of friction k.
 View Solution
View SolutionA body of mass m is hauled from the Earth's surface by applying a force F varying with the height of ascent y as F=2(ay−1)mg, whera a is a positive constant. Find the work performed by this force and the increment of the body's potential energy in the gravitational field of the Earth over the first half of the ascent.
View SolutionA block of mass m is pulled slowly by a minimum constant force on a rough (μ) horizontal surface through a distance x. Find work done by force F.
View SolutionA small object of mass 'm' is moved over a rough, curved surface as shown. The force which moves it along the dotted path shown is always tangential to the curved path. If the object moves with negligible speed, find the work done by the force F in moving it from A to B. The coefficient of friction between the object and the curved surface is μ.
 View Solution
View SolutionA block of mass m is slowly carried on a inclined plane by a force F which always acts along the tangent to the plane. If the co-efficient of friction between the block and incline be μ, then work done by force of friction while carrying block from bottom of the plane to the top will be :
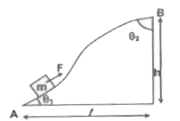 View Solution
View Solution

