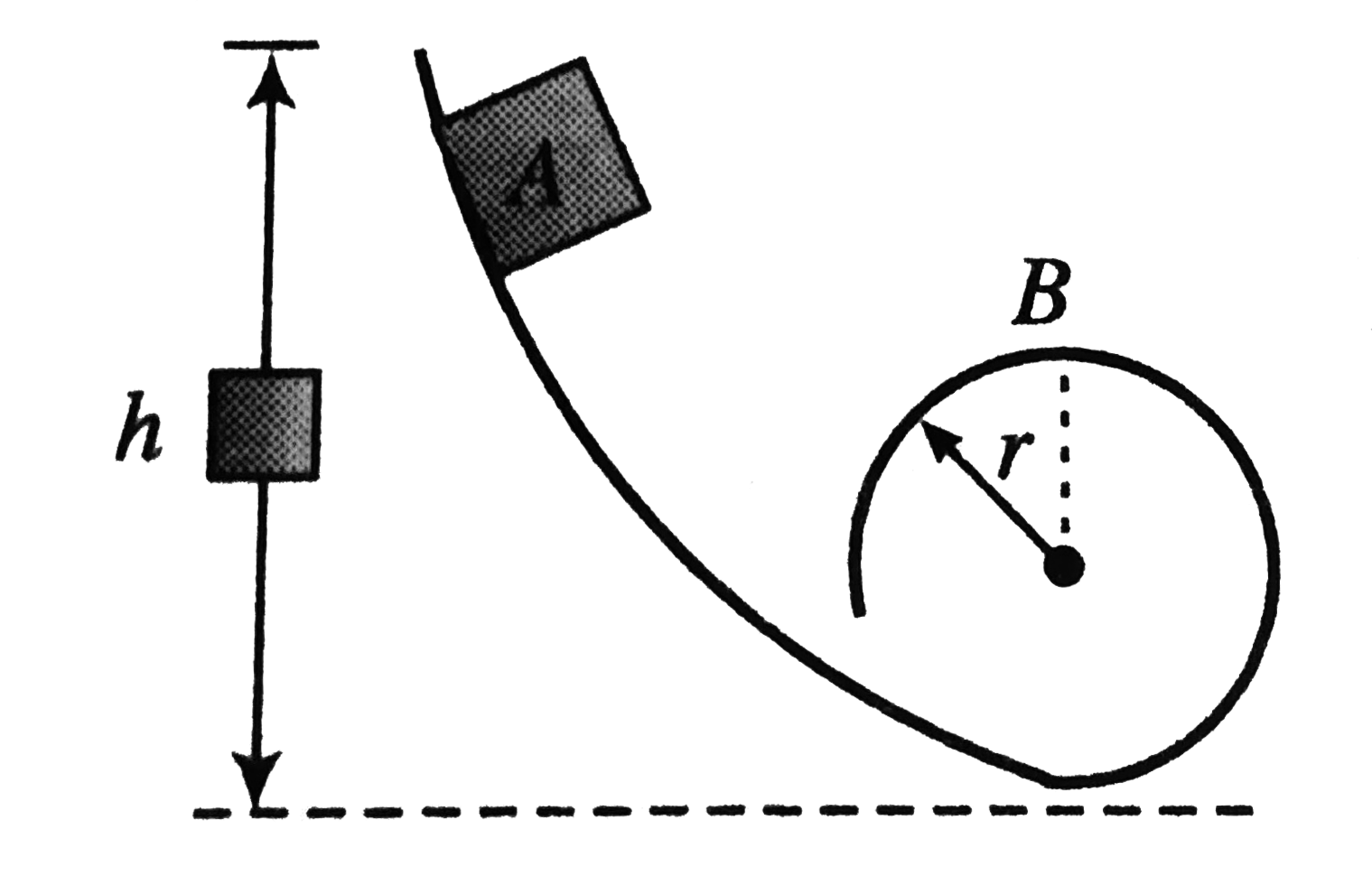
In the figure of problem 17 if the block starts from rest when R=5r, what is the reaction of the inner track on the sliding mass at the highest point ? From what height should it fall so that it may exert a force equal to its weight on the track at the highesth point ?
The correct Answer is:5 mg, 3r
Topper's Solved these Questions
- CENTRIPITAL AND CENTRIFUGAL FORCESBOOK - NN GHOSHCHAPTER - CENTRIPITAL AND CENTRIFUGAL FORCESEXERCISE - Exercises (A)
18 Videos
- CALORIMETRYBOOK - NN GHOSHCHAPTER - CALORIMETRYEXERCISE - All Questions
28 Videos
- COMPOSITION AND RESOLUTION OF VELOCITIESBOOK - NN GHOSHCHAPTER - COMPOSITION AND RESOLUTION OF VELOCITIESEXERCISE - Exercise
25 Videos
Similar Questions
In problem 17 if the mass m is allowed to fall from a height 2R, find the reaction of the track on the sliding mass the lowest point, at the highest point, at the mid-point. Take R:r=5:2
View SolutionA small block of mass m slides along a smooth track, as shown in fig. (i) If it starts from rest at P, what is the resulting force acting on it at Q ? (ii) at what height above the bottom of the loop should the block be released so that the force it exerts against the track at the top of the loop equals its weight?
View Solution
Knowledge Check
A cube of mass M starts of rest from point 1 at a height 4R, where R is the radius of the circular track. The cube slides down the frictionless track and around the loop. The force which the track exerts on the cube at point 2 is :
A3 MgBMgC2MgDCube will not reach the point 2A small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
AR/2BRCR/4D3R/4A mass m starting from A reaches B of a frictionless track. On reaching B, it pushes the track with a force equal to x times its weight, then the applicable relation is
A(a) h=(x+5)2rB(b) h=x2rC(c) h=rD(d) h=(x+12)r
As shown in the figure, a cube of mass m starts from rest from point 1 at a height 4R, where R is the radius of the circular track. The cube slides down the frictionless track and goes around the loop as shown. The force which the track exerts on the cube at point. 2 is βmg. Find β.
'(##CEN_KSR_PHY_JEE_C07_005_Q03##)'
View SolutionA small block of mass m slides along a smooth frictionless track as shown.
(a) If it starts from rest at P, what is the resultant force acting on it at Q?
(b) At what height above the bottom should the block be released so that the force it exerts against the track at the top of the loop equals its weight?
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
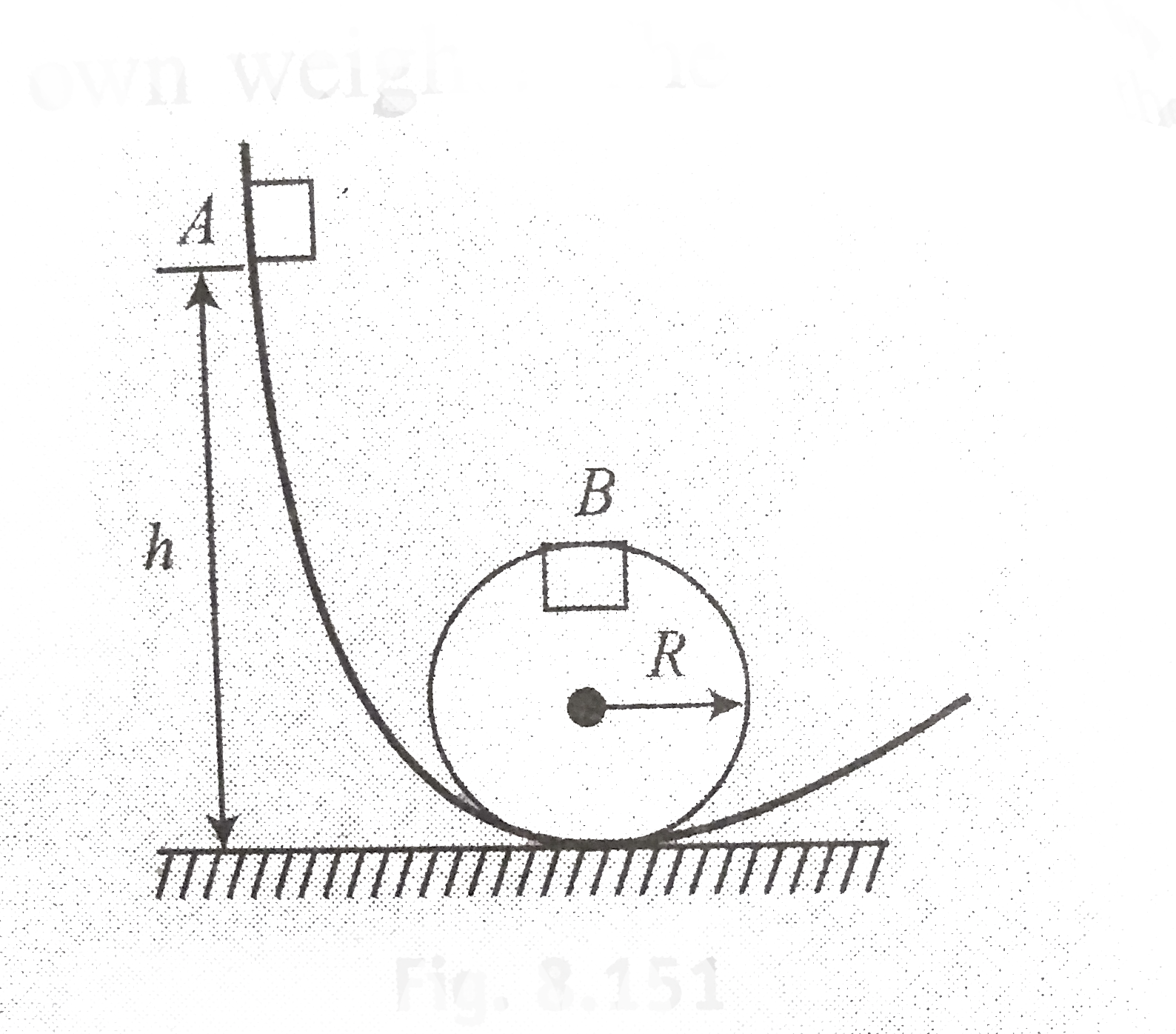
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
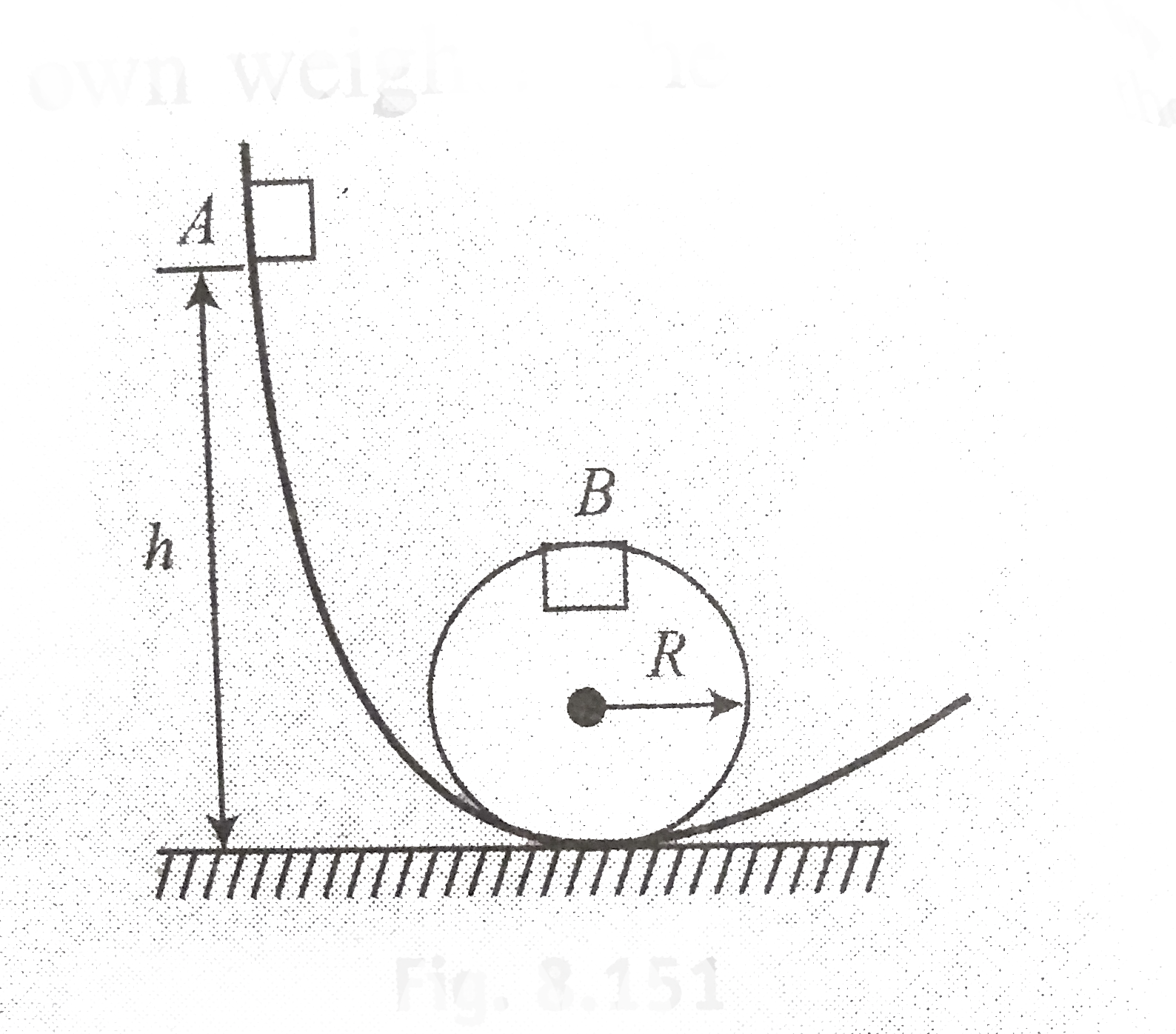
View SolutionA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View Solution