Calculate the moment of inertia of a cylinder of length 1.5m, radius 0.05m and density 8×103kg/m3 about the axis of the cylinder.
The correct Answer is:0.1178 kgm2
Step by step video, text & image solution for Calculate the moment of inertia of a cylinder of length 1.5 m, radius 0.05m and density 8 xx 10^(3) kg//m^(3) about the axis of the cylinder. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- SATURATED AND UNSATURATED VAPOURBOOK - NN GHOSHCHAPTER - SATURATED AND UNSATURATED VAPOUREXERCISE - All Questions
1 Videos
Similar Questions
Calculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
View SolutionCalculate the moment of inertia of a solid sphere of mass 10 kg and radius 0.5 m, rotating about an axis 0.2 m from the centre of the sphere .
View Solution
Knowledge Check
Moment of inertia of a hollow cylinder of mass M and radius r about its own axis is
A23Mr2BMr2C13Mr2D12Mr2The moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
A12M(a2+2b2)B12M(2a2+b2)C12M(a2+b2)D12M(a23+b212)Moment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
A23B32C√23D√32
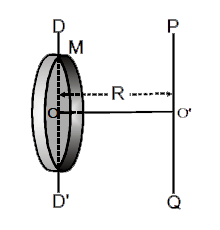
The moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
View SolutionWhat is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionCalculate the moment of inertia of a ring of mass 0.5 kg and radius 0.1 m rotating about a tangent (a) in its plane (b) perpendicular to its plane.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
