A pipe in the form of a half ring is placed on a horizontal surface. If it is rotated through a small angle, and then released, assuming that it rolls without sliding determine the period of oscillations. The center of gravity of such a body is at distance 2rπ) from the center where r is the radius of the ring.
Hint: (→–––(c)=αrˆi and
→ac=→ac+(→aG/c)tangent+(→aG/c)normal
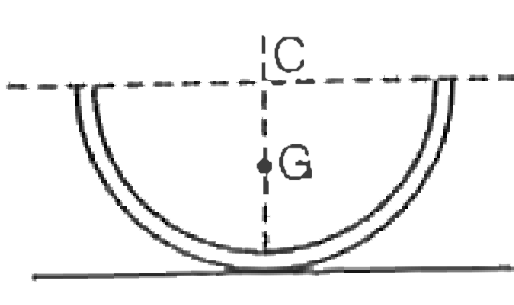
The correct Answer is:2n√(π−2)rg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions
17 Videos
Similar Questions
Knowledge Check
A ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VR
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View Solution
