find the density of air at any height and hence the height at which it is halved. Assume that the temperature reamins fixed throughout the atmosphere. The pressure at the earth's surface is and density
The correct Answer is:
Step by step video, text & image solution for find the density of air at any height and hence the height at which it is halved. Assume that the temperature reamins fixed throughout the atmosphere. The pressure at the earth's surface is P_(0) = 1.012 xx 10^(5) Nm^(-2) and density p_(o)=1.293 kg m^(-3) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The density of the atmosphere at sea level is 1.29kg/m3. Assume that it does not change with altitude. Then how high would the atmosphere extend ? g=9.8ms−2. Atmospheric pressure =1.013×105Pa.
View Solution(a) Pressure decreases as one ascends the atmosphere. If the density of air is ρ, What is the change in pressure dp over a differential height dh ? (b) Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the sureface of the earth is p0. (c ) If p0=1.03×105Nm−2,ρ0=1.29kgm−3andg=9.8ms−2, at what height will the pressure drop to (1/10) the value at the surface of the earth ? (d) This model of the atmosphere works for relatively small distance. Identify the underlying assumption that limits the model.
View Solution
Knowledge Check
- Question 1 - Select One
1 atmospheric pressure is taken as the pressure exerted by a mercury column of height 76 cm . Wh at is the approximate height of an air column that will produce one atmospheric pressure on its bottom ? [Assume that the temperature and density of a ir and th e value ofg remains constant throughout the a ir column .]
[ρmercury=13.6×103kg/m3 and ρair=1.3kg/m3]A8 kmB6 kmC5 kmD4 km - Question 2 - Select One
At N.T.P., the R.M.S velocity of hydrogen molecule is (P=1.013×105N/m2, Density of hydrogen=0.09kg/m3)
A1640 m/sB1738 m/sC1838 m/sD1938 m/s - Question 3 - Select One
The rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
A300ms−1B900ms−1C120ms−1D600ms−1
What would be the height of the atmosphere if the air density (a) were uniform and (b) decreased linearly to zero with height? Assume that at sea level the air pressure is 1.0 atm and the air density is 1.3 kg/m3
View SolutionA tank containing gasoline is sealed and the gasoline is under pressure P0 as shown in the figure. The stored gasoline hs a density of 660kgm−3. A sniper fires a rifle bullet into the gasoline tank, making a small hole 53m below the surface of gasoline. The total height of gasoline is 73m from the base. The jet of gasoline shooting out of the hole strikes the ground at a distance of 80m from the tank initially. If the pressure above the gasonline surface is (1.39)α×105N/m2 than α is- (The local atmospheric pressure is 105Nm−2)
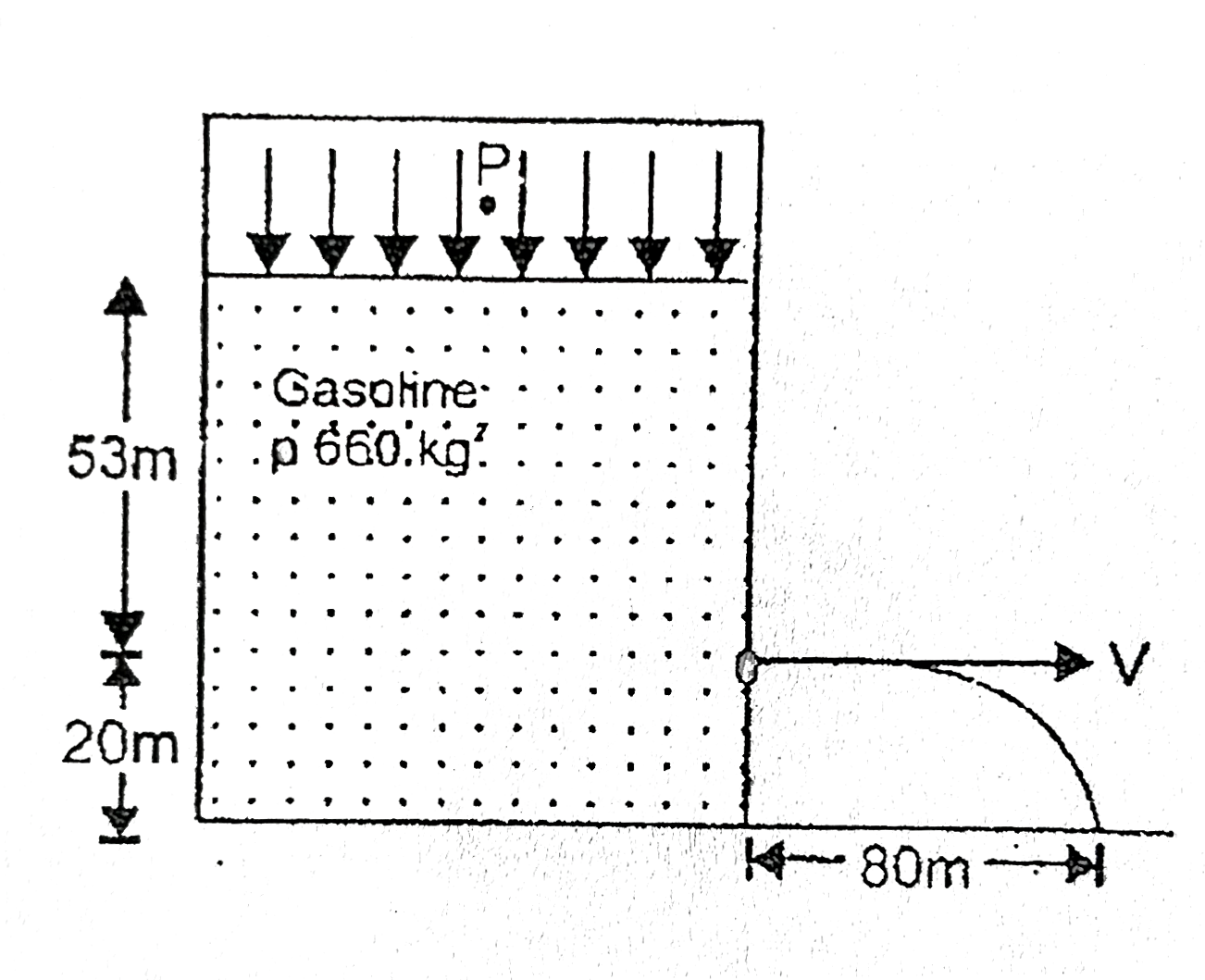 View Solution
View SolutionDiameter of a planet is 10d∘, its mean density is ρ∘4 and mass of its atmosphere is 10m∘ where d∘, ρ∘ and m∘ are diameter, mean density and mass of atmosphere respectively for the earth. Assume that mean density of atmosphere is same on the planet and the earth and height of atmosphere on both the planets is very small compared to their radius. Find the ratio of atmospheric pressure on the surface of the planet to that on the earth. If a mercury barometer reads 76 cm on the surface of the earth, find its reading on the surface of the planet.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionCalculate the pressure at a depth of 10 m in an Ocean. The density of sea water is 1030kg/m3. The atmospheric pressure is 1.01×105 pa.
View Solution

