A long metal rod of length I and density p is held vertically with its lower end touching sea-water of density p0. Calculate the time in which the whole of the rod will sink into water and the velocity of the rod. Negtect water resistance and assume vertical postion of the rod throughout its motion .
The correct Answer is:√2gl(1−p02pg),√plp0gcos−1(1−p0p)
Topper's Solved these Questions
Similar Questions
A rod of length 2 m is held vertically with one of its end on the floor. It is then allowed to fall. Calculate the speed of the other end when it strikes the floor. Assume that the end of the rod which is on the floor does not slip.
View SolutionA rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

View Solution
Knowledge Check
A rod of length L, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
A√2gLB√2gLC√3gLD√3gLA thin metal rod of length 0.5m is vertically straight on horizontal floor. This rod is falling freely to a side without slipping. The angular velocity of rod when its top end touches the floor is (nearly)
A7rads−1B4.2rads−1C3.5rads−1D2.1rads−1A rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
A2ms−1B1ms−1C4ms−1D1.5ms−1
A rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

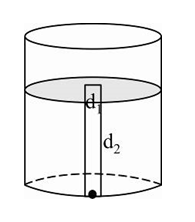
View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
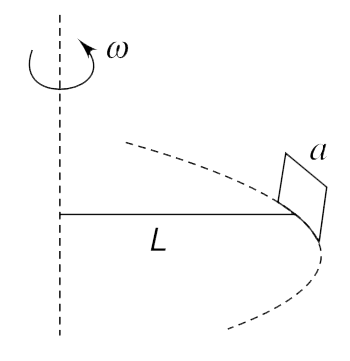
View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
View SolutionA rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
View SolutionA uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal.
View Solution
