Instantaneous velocity of an object varies with time as v=α−βt2. Find its position and acceleration as a function of time, also find the object's maximum positive displacement from the origin.
Step by step video & image solution for Instantaneous velocity of an object varies with time as v = alpha - beta t^(2). Find its position and acceleration as a function of time, also find the object's maximum positive displacement from the origin. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Practice Exercise96videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question18videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
The position x of a particle varies with time t according to the relation x=t3+3t2+2t. Find the velocity and acceleration as functions of time.
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View Solution
Knowledge Check
- Question 1 - Select One
A car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
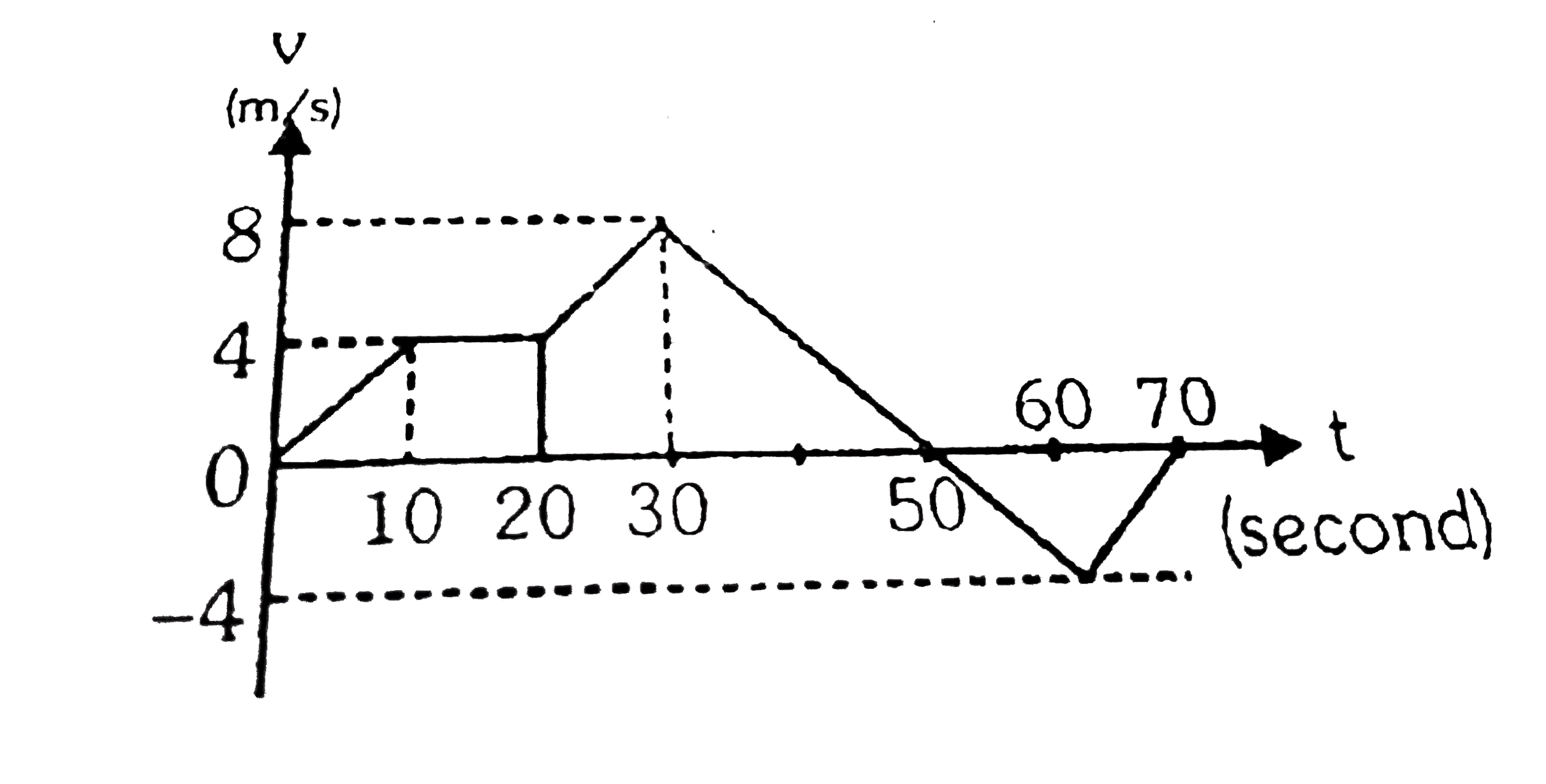
The maximum displacement from the starting position will be :-A200 mB250 mC160 mD165 m - Question 2 - Select One
The velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.A3ms−2B4ms−2C3.5ms−2D5ms−2
The velocity v of moving object varies with displacement u as v=3x^(2)-2 ,then the acceleration at x=2m is
View SolutionThe position of a particle varies with function of time as y=(4sint+3cost)m. Then the maximum displacement of the particle from origin will be
View SolutionThe velocity of an object varies as v=ht24. Calculate the change in position of the ball is time t.
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?View SolutionDraw the velocity-time graph of an object moving with uniform positive acceleration.
View SolutionParticle 's position as a function of time is given by x=−t2+4t+4 find the maximum value of position coordinate of particle.
View Solution

