A boy releases a toy plane from the top of a high hill of height H. Hill is so high that gravity varies with height from ground as , where h is the height from ground and R is the radius of earth. The engine of toy plane accelerates it in horizontal direction with acceleration . Find the position from the foot of hill where the plane lands and the time after which it lands.
The correct Answer is:
Step by step video, text & image solution for A boy releases a toy plane from the top of a high hill of height H. Hill is so high that gravity varies with height from ground as g = g_(0) (1 - (2h)/(R)), where h is the height from ground and R is the radius of earth. The engine of toy plane accelerates it in horizontal direction with acceleration a_(x) = bt^(2). Find the position from the foot of hill where the plane lands and the time after which it lands. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question18videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct35videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.83videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
Knowledge Check
- Question 1 - Select One
In the usual notation, the acceleration due to gravity at a height h from the surface of the earth is ………………
Ag(GM)(R+h)Bg=GM√R+h.Cg=GM(R+h)2Dg=GM(R+h)2 - Question 2 - Select One
In the usual notation, the acceleration due to gravity at a height h from the surface of the earth is ……………
Ag=GMR+hBg=GM√R+hCg=GM(R+h)2Dg=GM(R+h)2 - Question 3 - Select One
A body is released from a height 5R where R is the radius of the earth. Then that body reaches the ground with a velocity equal to
A√5gR3B√3gR5C√5gRD√3gR
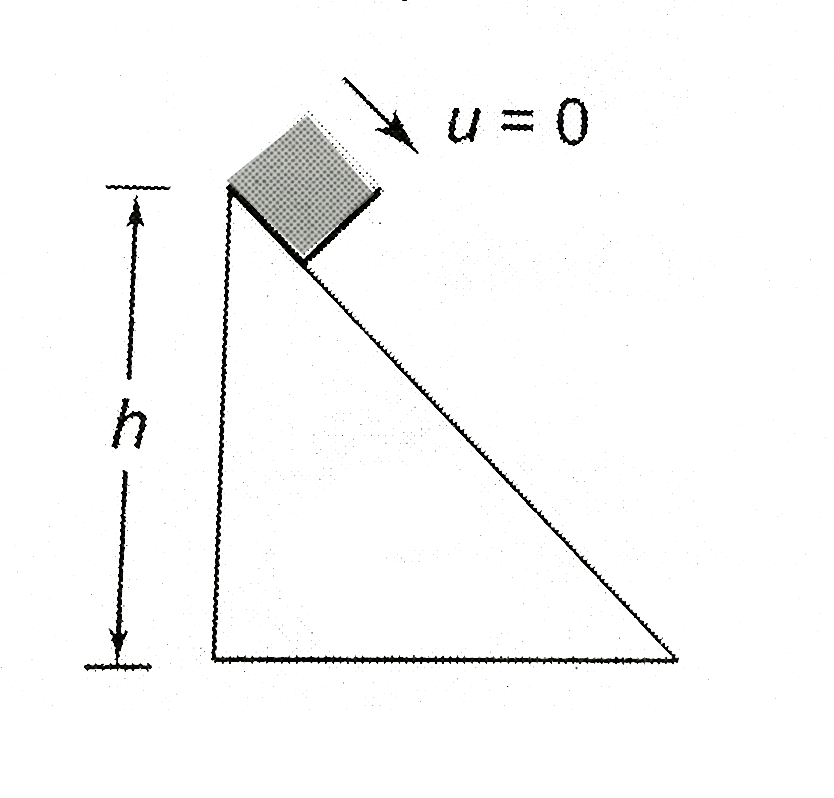
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.View SolutionThe acceleration due to gravity at a height h is given by gh=g(RR+h)2, where g is the accleeration due to gravity on the surface of earth. For h<<R, find the value of g using the Binomial theorem.
View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View SolutionA body is released from the top of a tower of height h. It takes t sec to reach the ground. Where will be the ball after time t2 sec?
View SolutionWhat will be the acceleration due to gravity at height h<<R . Where R is radius of earth and g is acceleration to gravity on the surface earth
View Solution

