For a particle moving along a straight line, the displacement x depends on time t as x=At3+Bt2+Ct+D. The ratio of its initial velocity to its initial acceleration depends on:
A & C
B & C
C
C and D
The correct Answer is:B
To solve the problem, we need to find the initial velocity and initial acceleration of the particle based on the given displacement equation and then determine the ratio of these two quantities.
1. Given Displacement Equation:
The displacement of the particle is given by:
x=At3+Bt2+Ct+D
2. Find Initial Velocity:
The velocity v is the first derivative of displacement x with respect to time t:
v=dxdt=ddt(At3+Bt2+Ct+D)
Differentiating term by term:
v=3At2+2Bt+C
To find the initial velocity v0, we evaluate v at t=0:
v0=3A(0)2+2B(0)+C=C
3. Find Initial Acceleration:
The acceleration a is the derivative of velocity v with respect to time t:
a=dvdt=ddt(3At2+2Bt+C)
Differentiating term by term:
a=6At+2B
To find the initial acceleration a0, we evaluate a at t=0:
a0=6A(0)+2B=2B
4. Calculate the Ratio of Initial Velocity to Initial Acceleration:
Now, we can find the ratio of initial velocity v0 to initial acceleration a0:
Ratio=v0a0=C2B
Final Answer:
The ratio of the initial velocity to the initial acceleration is:
C2B
The displacement of the particle is given by:
x=At3+Bt2+Ct+D
The velocity v is the first derivative of displacement x with respect to time t:
v=dxdt=ddt(At3+Bt2+Ct+D)
Differentiating term by term:
v=3At2+2Bt+C
To find the initial velocity v0, we evaluate v at t=0:
v0=3A(0)2+2B(0)+C=C
The acceleration a is the derivative of velocity v with respect to time t:
a=dvdt=ddt(3At2+2Bt+C)
Differentiating term by term:
a=6At+2B
To find the initial acceleration a0, we evaluate a at t=0:
a0=6A(0)+2B=2B
Now, we can find the ratio of initial velocity v0 to initial acceleration a0:
Ratio=v0a0=C2B
The ratio of the initial velocity to the initial acceleration is:
C2B
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Numerical111videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Advance MCQs with One or More Options Correct17videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question18videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
(a) If the initial velocity of a particle is u and collinear acceleration at any time t is at, calculate the velocity of the particle after time t.
(b) A particle moves along a straight line such that its displacement at any time t is given by s=(t3−6t2+3t+4)m. What is the velocity of the particle when its acceleration is zero?View SolutionA particle moves along a straight line such that its positionx at any time t is x=3t2−t3, where x is in metre and t in second the
View Solution
Knowledge Check
- Question 1 - Select One
For a particle moving along a straight line, the displacement x depends on time t as x=αt3+βt2+γt+δ. The ratio of its initial acceleration to its initial velocity depends
Aonly on α and βBonly on β and γConly on α and γDonly on α - Question 2 - Select One
For a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?A−9ms−1B−12ms−1C3ms−1D42ms−1 - Question 3 - Select One
The position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 sec
The acceleration time graph of a particle moving along a straight line is as shown in Fig.At what time the particle acquires its initial velocity?
View SolutionDisplacement of a particle moving in a straight line is represented as follows:
x=at3+bt2+ct+d Ratio of initial velocity to initial acceleration depends.View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
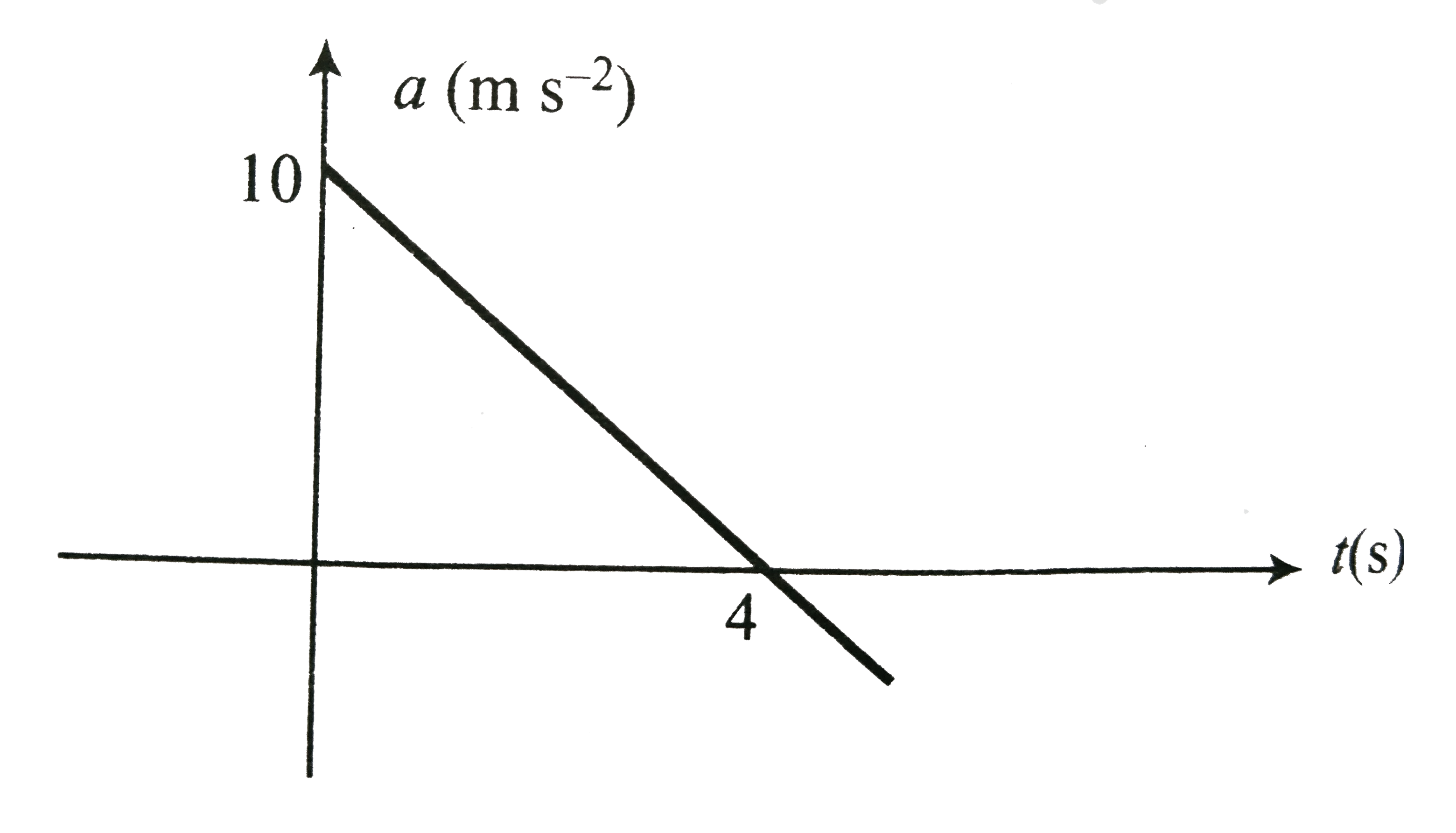 .View Solution
.View SolutionA particle moves along x-axis and its displacement at any time is given by x(t)=2t3−3t2+4t in SI units. The velocity of the particle when its acceleration is zero is
View Solution

