Each second a rabbit moves half the remaining distance from its nose to ahead of lettuce. Does the rabbit ever get to the lettuce ? What is the limiting value of the rabbit's velocity? Draw graphs showing the rabbit's position and average velocity versus time.
Step by step video & image solution for Each second a rabbit moves half the remaining distance from its nose to ahead of lettuce. Does the rabbit ever get to the lettuce ? What is the limiting value of the rabbit's velocity? Draw graphs showing the rabbit's position and average velocity versus time. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct35videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Numerical111videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Practice Exercise96videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
A stone is dropped into a river from a bridge 53.6 m above the water. Another stone is thrown vertically down 1.00 s after the first is dropped. The stones strike the water at the same time. (a) What is the initial speed of the second stone ? (b) Plot velocity versus time on a graph for each stone, taking zero time as the instant the first stone is released .
View SolutionA prototype of a rocket is fired from the ground. The rocket rises vertically up with a uniform acceleration of 54m/s2. 8 second after the start a small nut gets detached from the rocket. Assume that the rocket keeps rising with the constant acceleration.
(a) What is the height of the rocket at the instant the nut lands on the ground
(b) Plot the velocity – time graph for the motion of the nut after it separates from the rocket till it hits the ground. Plot the same velocity– time graph in the reference frame of the rocket. Take vertically upward direction as positive and g=10m/s2View Solution
Knowledge Check
- Question 1 - Select One
The velocity time graph of a particle moving along a straight line is shown in the figure. In the time interval from t=0 to t=8 second, answer the following three question.

The value of magnitude of maximum velocitymagnitude of average velocity for the given time interval is :A89B83C169D163 - Question 2 - Select One
Consider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time t1, the particle is at point P, where its co-ordinate is x1 and at time t2, the particle is at point Q, where its co-ordinate is x2. The displacement during the time interval from t1 to t2 is the vector from P to Q, the x-component of this vector is (x2−x1) and all other components are zero.
It is convenient to represent the quantity x2−x1 the change in x by means of a notation Δ, thus Δx=x2−x1 and Δt=t2−t1.
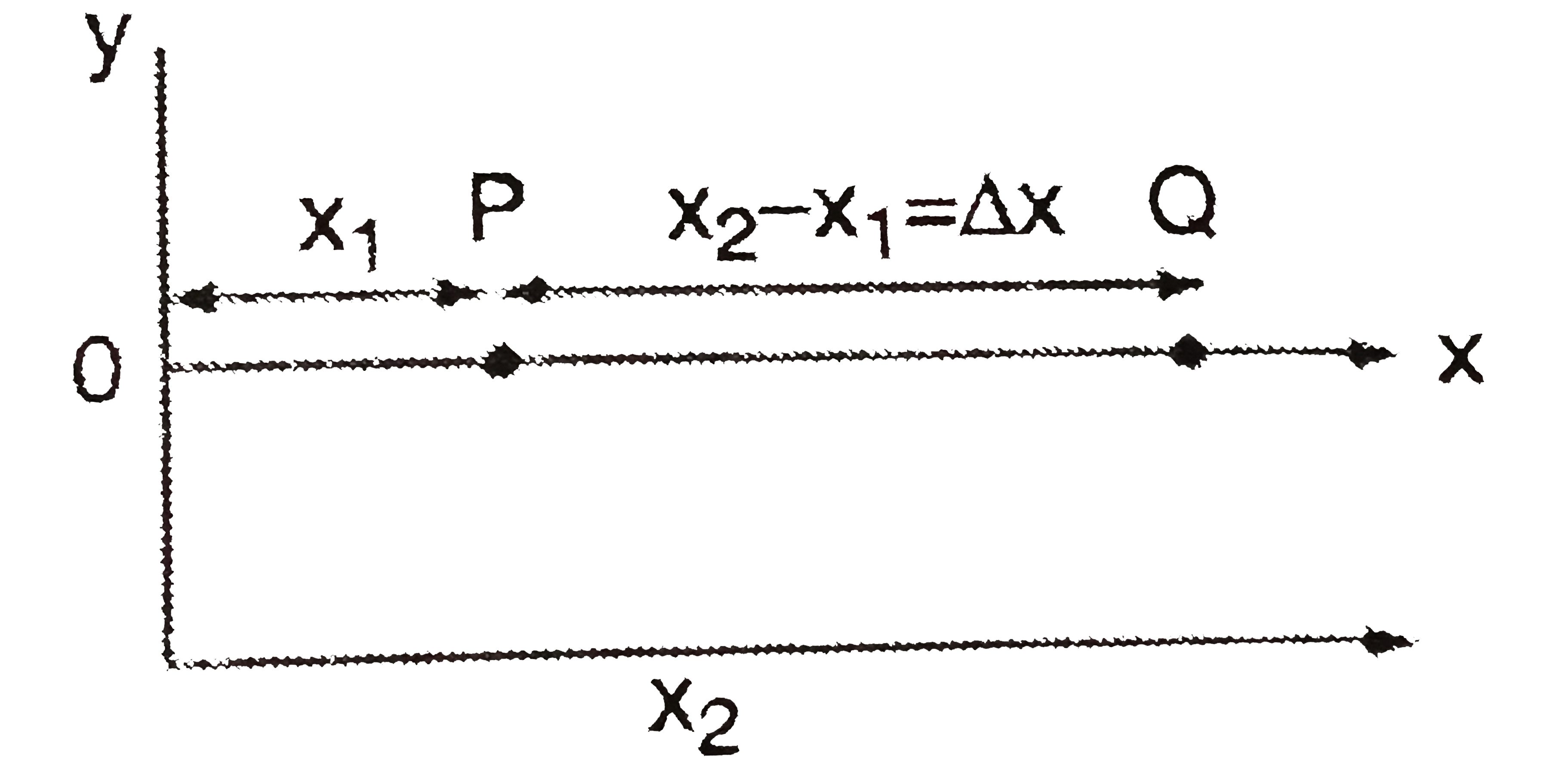
The average velocity ¯¯¯V=x2−x1t2−t1=ΔxΔt
A particle moves half the time of its journey with u. The rest of the half time it moves with two velocities v1 and v2 such that half the distance it covers with v1 and the other half with v2. The net average velocity is: (Assume straight line motion)Au(v1+v2)+2v1v22(v1+v2)B2u(v1+v2)2u+v1+v2Cu(v1+v2)2v1D2v1v2u+v1+v2 - Question 3 - Select One
The fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
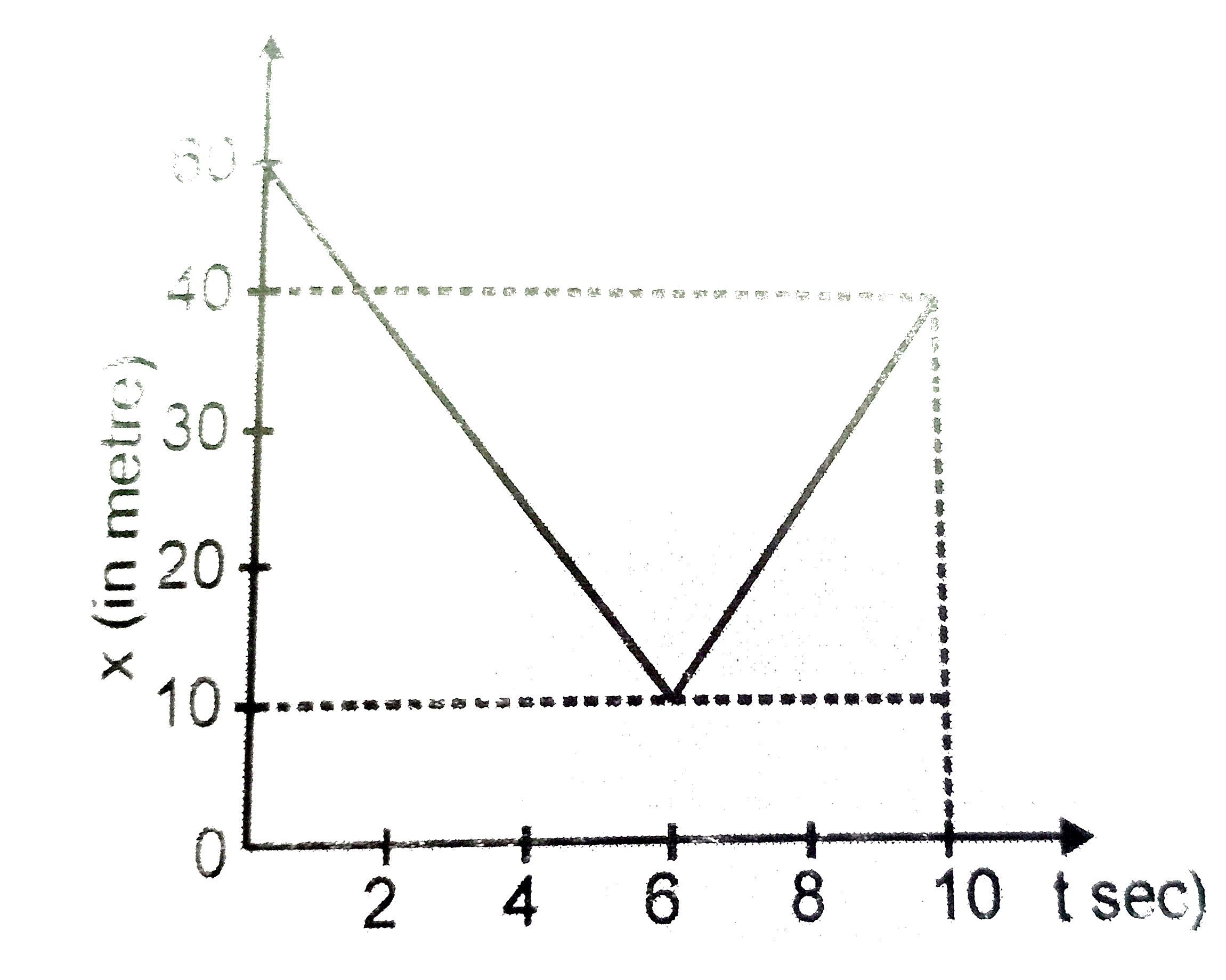 A2ms−1B4ms−1C6ms−1D8ms−1
A2ms−1B4ms−1C6ms−1D8ms−1
A particle moves for total time T sec in a straight line in three consecutive parts such that its acceleration during the first, second and third parts is in the ratio 1:2:7. The distances covered in the first and the third parts are a and b meters while the time taken for each of the is tseconds. Find the average velocity of the particle during the second part.
View SolutionA long straight copper wire, of circular cross ection, contains n conduction electrons per unit volume, each of charge q. Show that the current l in the wire is given by
l=nqvπa2
where v is the drift velocity and a is the radius of the wire.
At a radial distance r from the axis of the wire, what is the direction of the magnetic field B due to the current l? Assuming that the magnitude of the field is B=μ0l/2πr(r≥a), obtain an expression for the Lorentz force F on an electron moving with the drift velocity at the surface of the wire.
If l=10 A and a = 0.5mm, calcualte the magnitude of (a) the drift velocity and (b) the forcce, given that for copper, n=8.5×1028m−3View SolutionThe figure shows the snapshot at time t=0 of a transverse pulse travelling on a string in positive x direction.
(a) Sketch the pulse at a slightly later time.
(b) With the help of the given sketch draw a graph of velocity of each string segment versus position. Take upward direction as positive.
 View Solution
View SolutionA particle moves in a straight line. Figure-1.21 shows the distance traversed by the particle as a function of time t.Using the graph, find (a)the average velocity of the point during the time of motion, (b) the maximum velocity, (c) the time t=t0 at which the instantaneous velocity is equal to the mean velocity averaged over the first t0 seconds.
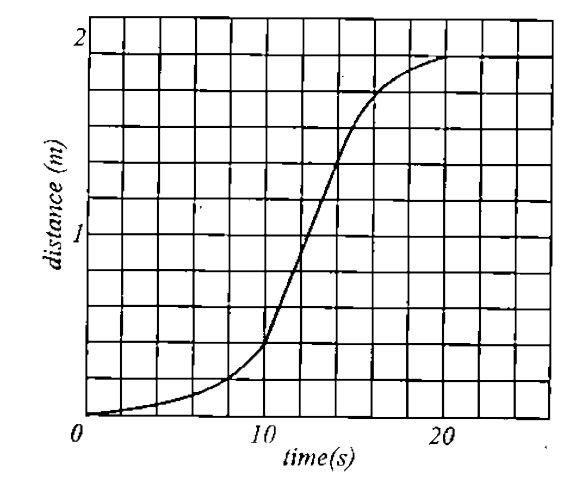 View Solution
View SolutionA particle moves along a horizontal path, such that its velocity is given by v=(3t2−6t)m/s, where t is the time in seconds. If it is initially located at the origin O, determine the distance travelled by the particle in time interval from t=0 to t=3.5s and the particle's average velocity and average speed during the same time interval.
View Solution

