The velocity of a particle moving on the x− axis is gienv by v=x2+x( for x>0) where v is in m/s and x is in m. Find its acceleration in m/s2 when passing through the point x=2m
0
5
11
30
The correct Answer is:D
Step by step video, text & image solution for The velocity of a particle moving on the x- axis is gienv by v=x^(2)+x( for xgt0) where v is in m//s and x is in m. Find its acceleration in m//s^(2) when passing through the point x=2m by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Advance MCQs with One or More Options Correct17videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.83videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct35videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
The velocity of a particle moving on the x-axis is given by v=x2+x, where x is in m and v in m/s. What is its position (in m) when its acceleration is 30m/s2.
View SolutionThe velocityof a particle that moves in the positive X- direction varies with its position, as shown in figure-1.22. Find its acceleration in m/s2 where x=6m
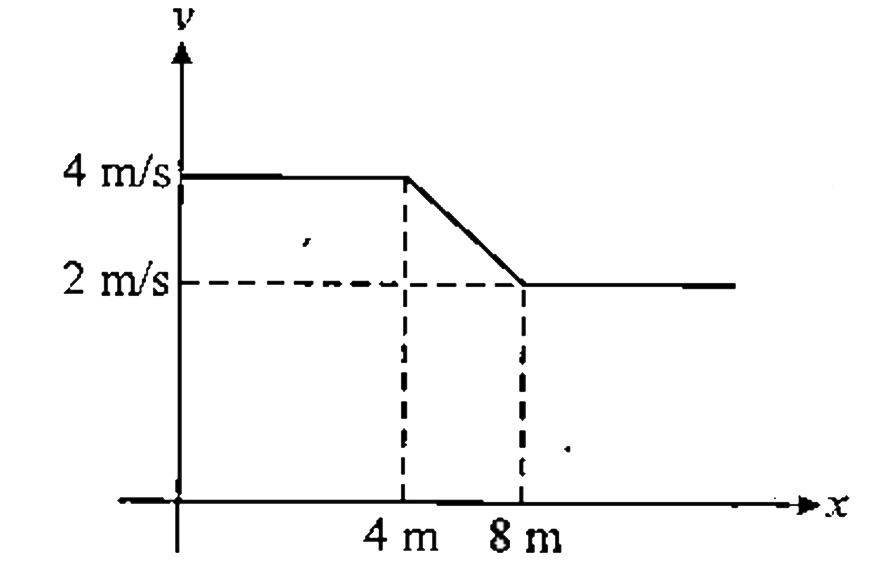 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
A0m/s2B2m/s2C3m/s2DNone of these - Question 2 - Select One
The velocity of a particle defined by the relation v = 8 -0.02x, where v is expressed in m/s and x in meter. Knowing that x = 0 at t = 0, the acceleration at t=0 is
A−0.16m/s2B−0.02m/s2C7.08m/s2D8m/s2 - Question 3 - Select One
Acceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.Av=2√2−x2Bv=3√1−x2Cv=2√1−x3Dv=2√1−x2
The velocity of a body moving in a straight line is given by v=(3x2+x)m/s . Find acceleration at x=2m.
View SolutionConsider the v-t diagram of a particle moving along x axis as shown below.Velocity is in m/s and time is in seconds v 4
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 View Solution
View Solution

