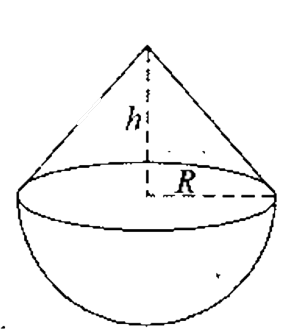
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:

1.5R

$\sqrt{3} R$

$3 R$

$2 \sqrt{3} R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A uniform solid right circular cone of base radius $R$ is joined to a uniform solid hemisphere of radius $R$ and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

A $1.5 R$
B $\sqrt{3} R$
C $3 R$
D $2 \sqrt{3} R$
Question 2 - Select One
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
A $(R^{2} + R + 1) (2 - R) = 1$
B $(R^{2} - R - 1) (2 - R) = 1$
C $(R^{2} - R + 1) (2 - R) = 1$
D $(R^{2} + R - 1) (2 - R) = 1$
Question 3 - Select One
Two solid right cones of equal height and radii $r_{1}$ and $r_{2}$ are melted and made to form a solid sphere of radius R. Then the height of the cone is
A $\frac{4 R^{2}}{r_{1}^{2} + r_{2}^{2}}$
B $\frac{4 R}{r_{1} + r_{2}}$
C $\frac{4 R^{3}}{r_{1}^{2} + r_{2}^{2}}$
D $\frac{R^{2}}{r_{1}^{2} + r_{2}^{2}}$

PHYSICS GALAXY - ASHISH ARORA-LINEAR MOMENTUM & ITS CONSERVATION-Numerical MCQ s

Home
Ask Doubt
Profile

A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

Two solid right cones of equal height and radii r1 and r2 are melted and made to form a solid sphere of radius R. Then the height of the cone is

PHYSICS GALAXY - ASHISH ARORA-LINEAR MOMENTUM & ITS CONSERVATION-Numerical MCQ s

A uniform solid right circular cone of base radius $R$ is joined to a uniform solid hemisphere of radius $R$ and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

Two solid right cones of equal height and radii $r_{1}$ and $r_{2}$ are melted and made to form a solid sphere of radius R. Then the height of the cone is