Find the centre of mass of a uniform solid cone.
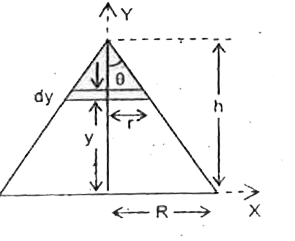
Let us consider a uniform solid cone of mass M, radius R and height h.
Xcm=0 (by symmetry)
Let us consider a small element (disc) of mass .dm., radius r and thickness dy at a distance y the from base as showm.
Then, ρ=3MπR2h=dmπr2dy
dm=3Mr2R2hdy
YCM=1M∫ydm=1M∫y3Mr2R2hdy=3R2h∫yr2dy
=3h∫h0y(1−yh)2dy [∵h−yr=hR⇒r=(1−yh)R]
On solving, we get YCM=h4
∴ C.M. of a uniform solid cone is (0,h4) from the centre of base.
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 10 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 18 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
Knowledge Check
The acceleration of the centre of mass of a uniform solid disc rolling down an inclined plane of angle θ is
A13gsinθB23gsinθCgsinθD14gsinθFind the centre of mass of a uniform I - shaped lamina (a thin flat plate) with dimensions as shown in figure. The mass of lamina is 3 kg
 A(1,1)B(32,12)C(56,56)D(32,32)
A(1,1)B(32,12)C(56,56)D(32,32)
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
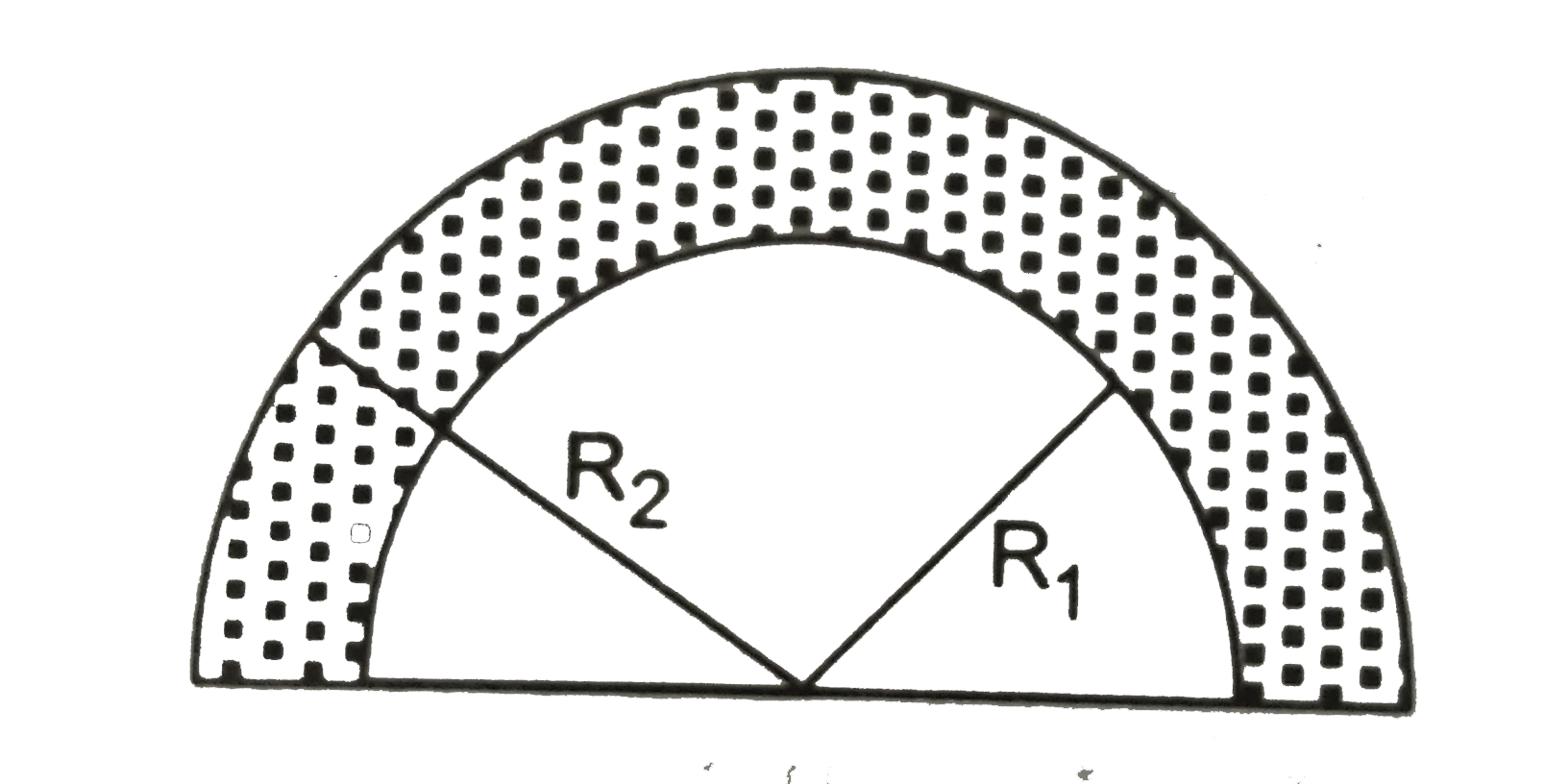
View SolutionFind the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1andR2.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) origine with dimensions as shown in figure. The mass of lamina is 3 kg.

View SolutionFind the centre of mass of as uniform L -shaped lamina (a thin flat plate) with dimensions as shown in figure. The mass of lamina is 3kg.

View Solution