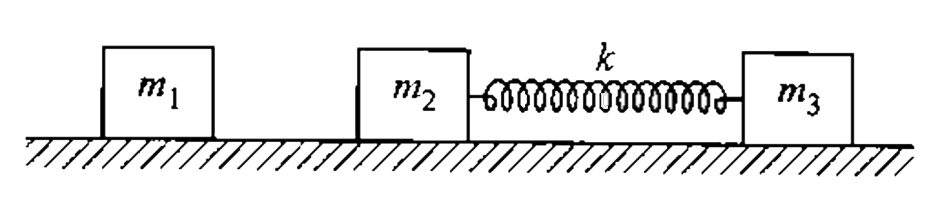
Mass $m_{1}$ hits $m_{2}$ with inelastic impact (e=0) while slliding horizontally with velocity v along the common line of centres of three equal mass as shoun in fugure $- 4.155 .$ Initially, masses $m_{2}$ and $m_{3}$ are stationary and the spring is unstressed. Find:

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $[\frac{v}{2}, 0 \frac{2}{9} m v^{2}, \frac{m v^{2}}{72}, \frac{\sqrt{m v^{2}}}{6 k}]$

Answer

Step by step video, text & image solution for Mass m_(1) hits m_(2) with inelastic impact (e=0) while slliding horizontally with velocity v along the common line of centres of three equal mass as shoun in fugure -4.155. Initially, masses m_(2) and m_(3) are stationary and the spring is unstressed. Find: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Three particles each of mass 'm' can slide on fixed frictionless circular track in the same horizontal plane as shown in the figure. Particle $m_{1}$ moves with velocity $v_{0}$ and hits particle $m_{2}$ , the coefficient of restitution being $θ = 1 / 2$ . AsSigmae $m_{2}$ and $m_{3}$ are initially in rest and lie along a radial line before impact and the spring is initially Unstretched. Then,

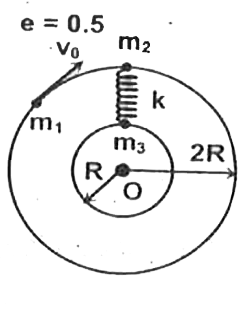
The velocity of $m_{3}$ when extension in the spring is maximum
A $\frac{1}{10} v_{0}$
B $\frac{3}{10} v_{0}$
C $\frac{7}{10} v_{0}$
Dnone of these
Question 2 - Select One
There particles each of mass $m$ can slide on fixed frictioless circular tracks in the same horizontal plane as shown. Particle $m_{1} (= m)$ moves with velocity $v_{0}$ and hits particle $m_{2} (= m)$ , the cofficient of restitution being $e = 0.5$ . Assume that $m_{2}$ and $m_{3} (= m)$ are at rest initially and lie along a radial line before impact, and the spring is initially unstretched.

Velocity of $m_{2}$ immediately after impact is
A $\frac{v_{0}}{4}$
B $\frac{3 v_{0}}{4}$
C $\frac{v_{0}}{2}$
D $\frac{3 v_{0}}{2}$
Question 3 - Select One
Three point like equal masses $m_{1}, m_{2}$ and $m_{3}$ are connected to the ends of a massless rod of length $L$ which lies at rest on a smooth horizontal plane. At $t = 0$ , an explosion occurs between $m_{2}$ and $m_{3}$ , and as a result, mass $m_{3}$ is detached from the rod, and moves with a known velocity v at an angle of $30^{\circ}$ with the $y$ -axis. Assume that the masses $m_{2}$ and $m_{3}$ are unchanged during the explosion. What is the velocity of the centre of mass of the system consisting of three masses, after the expulsion?

A $\frac{v}{4} (ˆ i - 3 ˆ j)$
B $\frac{v}{4} (- ˆ i + \sqrt{ˆ j})$
C $- v$
Dnone of these