Mass m1 hits & sticks with m2 while sliding horizontally with velocity v along the common line of centres of the three equal masses (m1=m2=m3=m). Initially masses m2 and m3 are stationary and the spring is unstretched. Find
(a) the velocities of m1,m2 and m3 immediately after impact.
(b) the maximum kinetic energy of m3.
(c) the minimum kinetic energy of m2.
(d) the maximum compression of the spring.

The correct Answer is:(a) u/2,mu/2; (b) 2mv2/9;(c)mv2/72;(d)x=√m/6kv
Just before collision
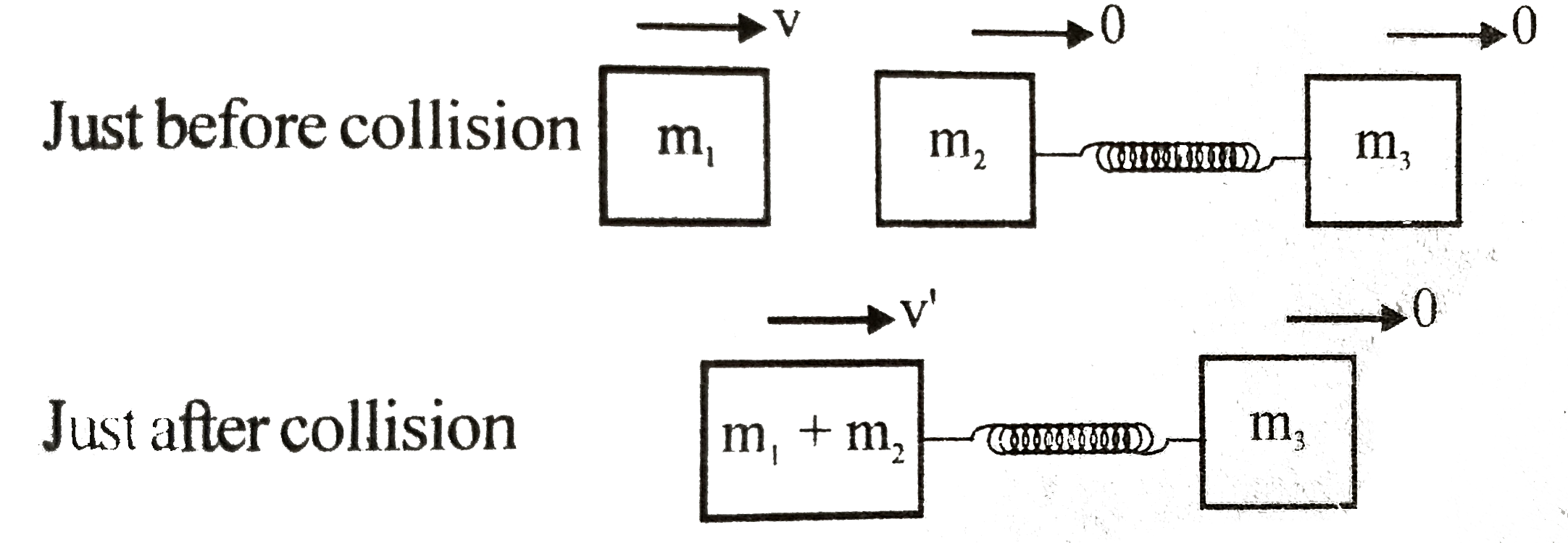
(a) We can use conservation of momentum as spring force is not an impulsive force.
⇒mv+0=(2m)v'⇒=v2
⇒vm1=v2,vm2=v2,vm3=0
(b) Looking from CM frome of refernce
vCM=(2m)v'+m(0)2m+m=23v'=v3
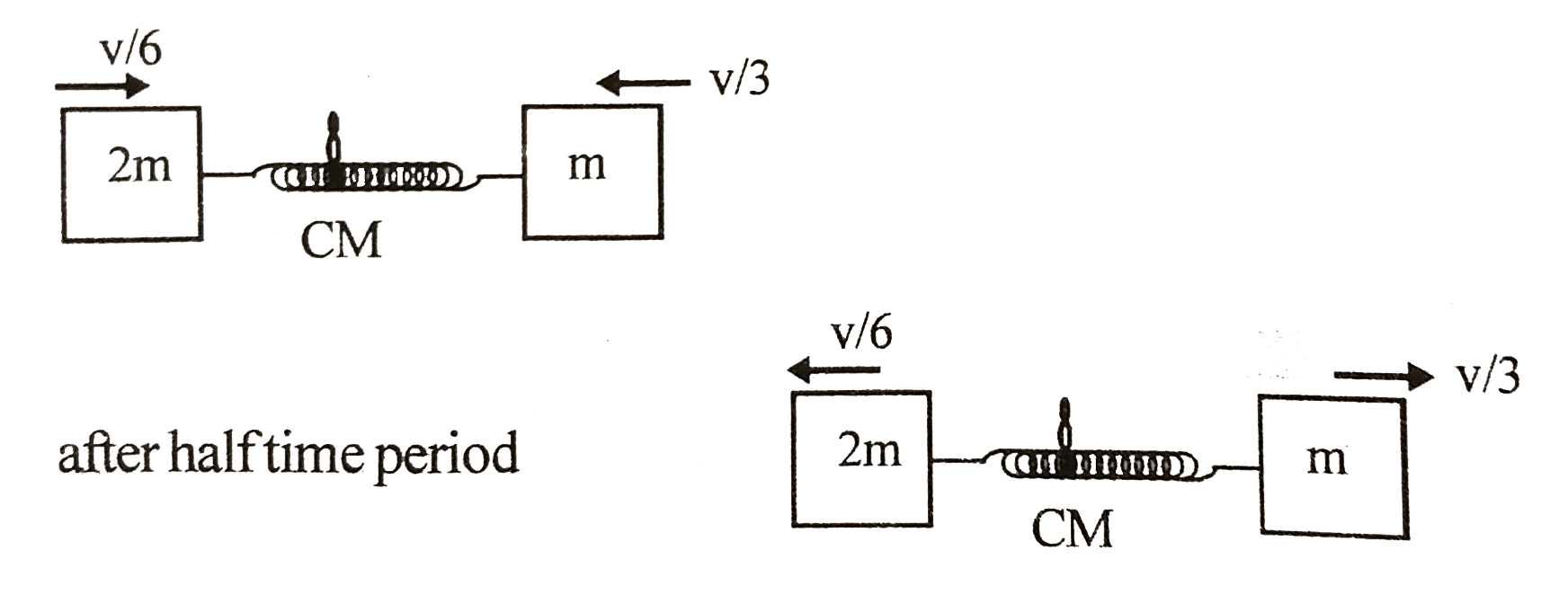
(Both the blocks will execute SHM of same time period in CM frome of reference)
⇒(vm3)max=v3+vCM=v3+v3=2v3
⇒(KEm3)max=12m(v3)2max=12m(2v3)2=2mv29
(c) (vm2)min=v3−v6=v6
⇒(KEm2)min=12m(v2)2min=12m(v6)2=mv272
(d) At the time of maximum compression, both blacks will be at rest in CM frame of reference
⇒12kx2max=12(2m)(v6)2+12m(v3)2
⇒12Kx2max=112mv2
⇒xmax=v√m6k
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (JEE-ADVANCED Previous Year Questions)
11 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (Comprehension)
3 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2[MATRIX TYPE]
2 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
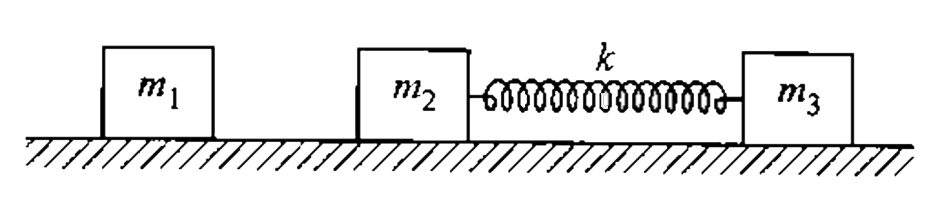
Mass m1 hits m2 with inelastic impact (e=0) while slliding horizontally with velocity v along the common line of centres of three equal mass as shoun in fugure −4.155. Initially, masses m2 and m3 are stationary and the spring is unstressed. Find:
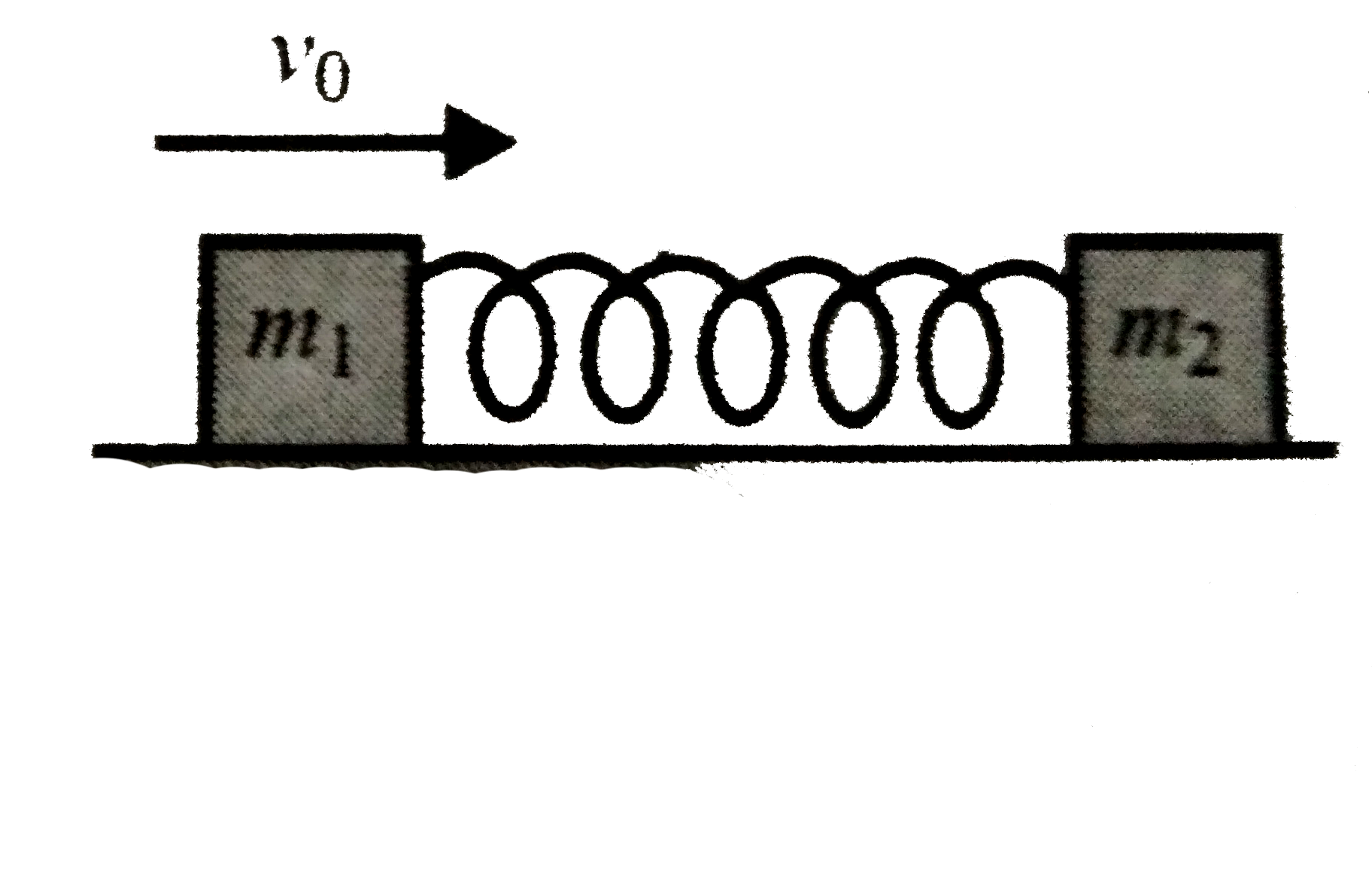
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
View Solution
Knowledge Check
Two bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
A√m1:√m2Bm1:m2Cm2:m1Dm21:m22If a lighter body (mass M1 and velocity V1 ) and a heavier body (mass M2 and velocity V2) have the same kinetic energy, then-
AM2V2<M1V1BM2V2=M1V1CM2V1=M1V2DM2V2>M1V1The centre of masses of three particles of mass m1=m2=m3=1 kg at the corners of an equilateral triangle of side 1 m will be -
A0.50m, 0.29mB0.43m, 0.50mC0.25m, 0.25mD0.22m, 0.22m
Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.

View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionFind the acceleration of masses m1,m2 and m3 shown in figure-2.119 just after the string is cut at point A.
[0,(1+m1m2)g,g]
View Solution
