Two cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
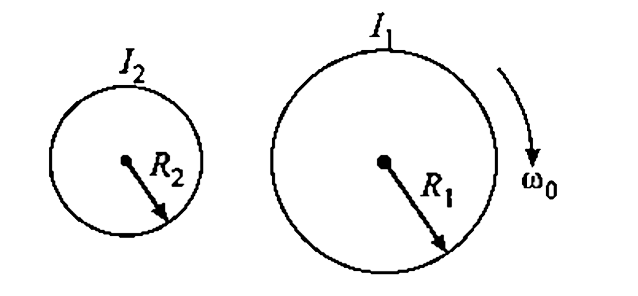
Step by step video & image solution for Two cylinders having radiii R_(1) and R_(2) and rotational inertia I_(1) and I_(2) respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityomega_(0). The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity omega_(2) of the small cylinder in terms of I_(1) , I_(2) , R_(1) , R_(2) and omega_(0). (b) Is total angular momentum conserved in this case ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Practice exercise
34 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions
Find the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View SolutionCan a single force applied to a body change both its translational and rotational motion? Explain.
View SolutionA packet of 150kg is released from an air plane travelling due east at an altitude of 7200 m with a ground speed of 100 m/s. The wind applies a constant force on the packet of 300 N directed horizontally in the opposite direction to the plane's flight path. Where and when does the packet hit the ground, (with respect to the release location and time)
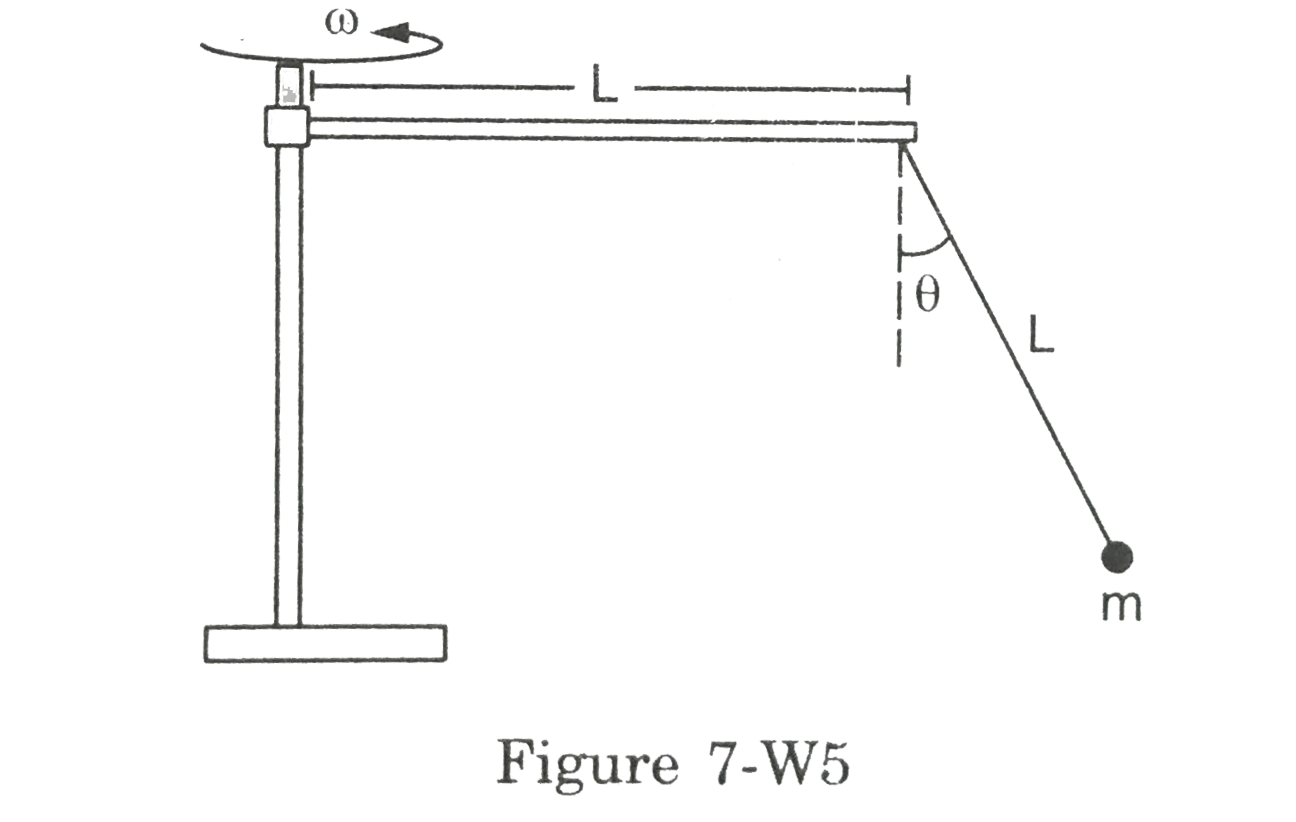
View SolutionFigure shows as rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball ofmass m is spuspended by a string angular also of length 20 cm from the other end of the rod. If the angle θ made by the stirng with the vertical is 300. find the anglular speed of the rotation. Take g=10ms2
View SolutionFigure shows two cylinders of raddi r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slipover each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the sylinders after the slipping ceases.

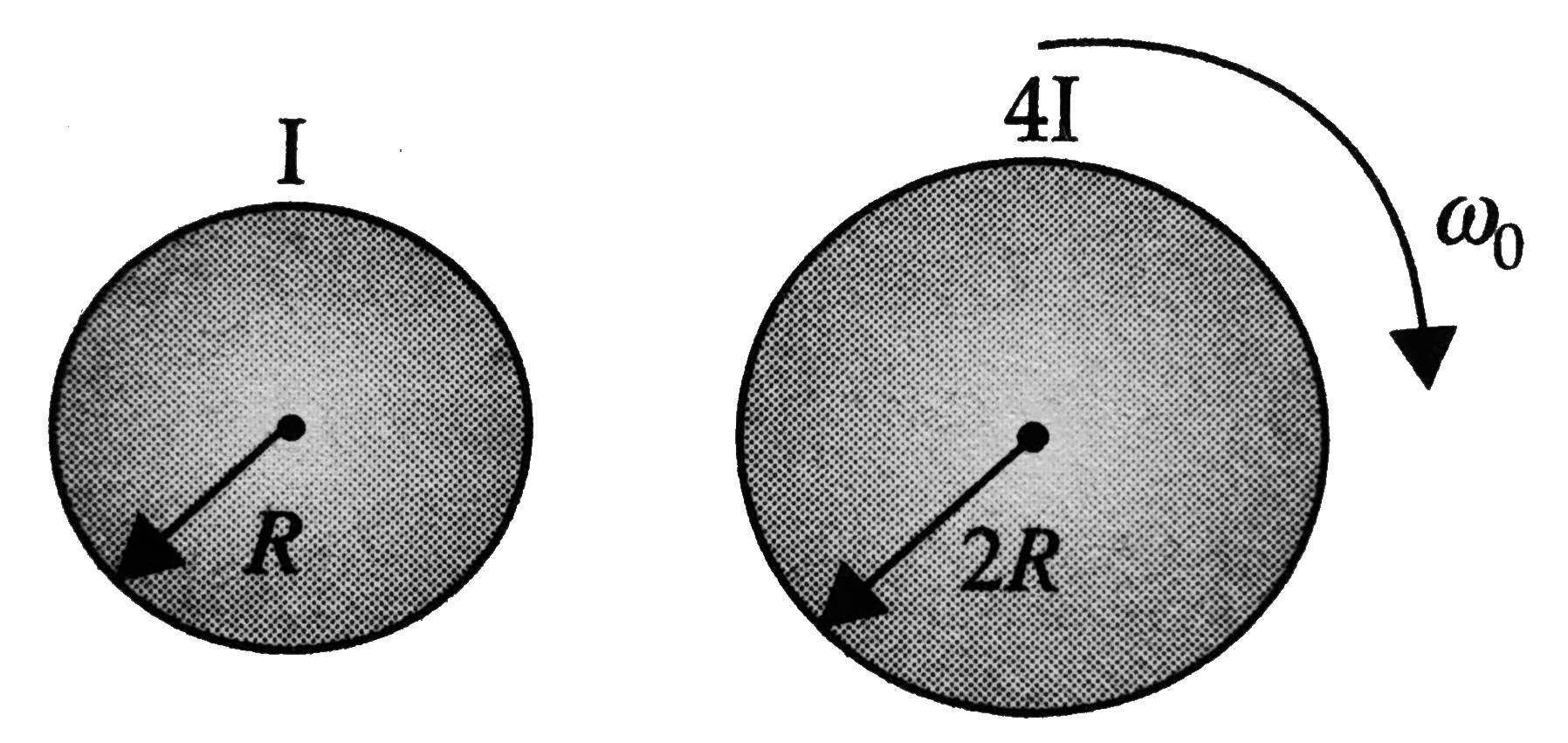
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
View SolutionTwo discs of moment of inertia I_(1) and I_(2) and angular speeds omega_(1) and omega_(2) are rotating along the collinear axes passing through their center of mass and perpendicular to their plane. If the two are made to rotate combindly along the same axis the rotational K.E. of system will be
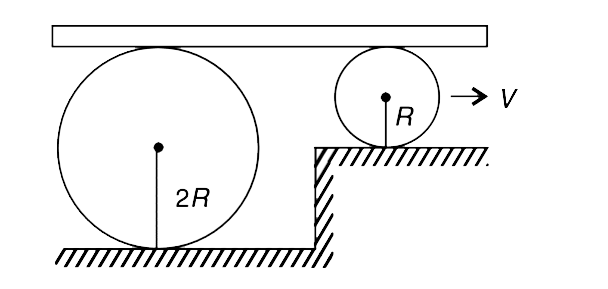
View SolutionIn the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity v. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
View SolutionThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v_(1) . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)
View SolutionThe axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v_(1) . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I If omega is final angular velocity of the cylinder, then
View SolutionTwo cylinders with radii r1 and r2 and rotational inertia I1 and I2 are supported on their horizontal axles. The first one is set in rotation with angular velocity ε. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]
View SolutionA solid cylinder of mass 20 kg rotates about its axis with angular velocity of 100 radian s^(-1) . The radius of the cylinder is 0.25m . The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity omega_(0)(=40 sqrtpi" rad s"^(-1)) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is mu(=2). Then, how many rotations will the cylinder make before it comes to rest?
View SolutionTwo discs of moment of inertia I_(1) and I_(2) are rotating separately with angular velocities omega_(1) and omega_(2) respectively about perpendicular axis passing through their centres. If these two rotating discs are connected coaxially then the rotational kinetic energy of the composite system will be
View SolutionFigure shows two cylinders of radii r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.

View Solution
