Figure shows two cylinders of raddi r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slipover each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the sylinders after the slipping ceases.

When slipping ceases, the linear speeds of the points of contact of the two cylinders will be equal. If the ω1andω2 be the respective angular speeds, we have
ω'1r1=ω'2=r2……….i
The change in the angular speed is brought about by the frictioN/Al force which acts as long as the slipping exists. If this force f acts for a time t, the torque on the first cylinder is _1 and that on the second is _2. Assuming ω1r1>ω2r2 the corresponding angular impluses are −_1tand_2t. We therefore have
−_1t=I1(ω'1−ω1)
and_2t=I2(ω'2=ω2)
or −I1r1(ω'1−ω1)=I2r2(ω'2−ω2)........ii
Solving i and ii
ω'1=I1ω1r2+I2ω2r1I2r21+I1r22r2andω'2=I1ω1r2+I2ω2r1I2r21+I1r22
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Two horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
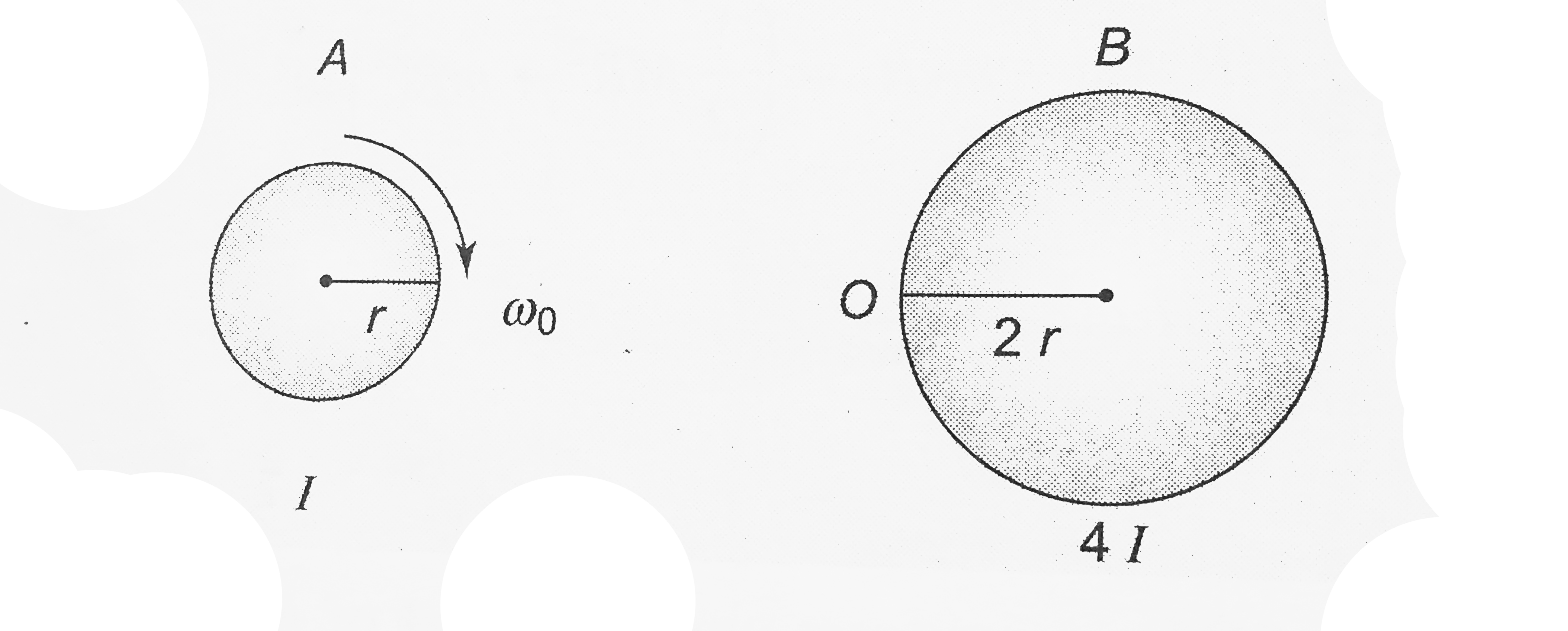
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View Solution
Knowledge Check
Two discs of moments of inertia I1 andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 andω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1≠ω2
ADoes the law of conservation of angular monentum apply to the situation ? Why ?BFind the angular speed of the two disc system .CCalculate the loss in kinetic energy of the system in the the process.DAccount for this loss.Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. What is the loss in kinetic energy of the system in the process?
AI1I2(ω1−ω2)22(I1+I2)BI1I2(ω1−ω2)2I1+I2CI1I2(ω1+ω2)2I1−I2DI1I2(ω1+ω2)22(I1−I2)Two discs of moment of inertia I1 and I2 about their respectively axes (normal) to the disc and passing through the centre) , and rotating with angular speed ω1 and ω2 are brought into contact face to face with their axes of rotation coincident .
What is the loss in kinetic energy of the system in the process ?AI1I2(ω1−ω2)22(I1+I2)BI1I2(ω1−ω2)2(I1+I2)CI1I2(ω1+ω2)2(I1−I2)DI1I2(ω1+ω2)22(I1−I2)
Two cylinders with radii r1 and r2 and rotational inertia I1 and I2 are supported on their horizontal axles. The first one is set in rotation with angular velocity ε. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes, rotating with angular frequencies, ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be A.
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
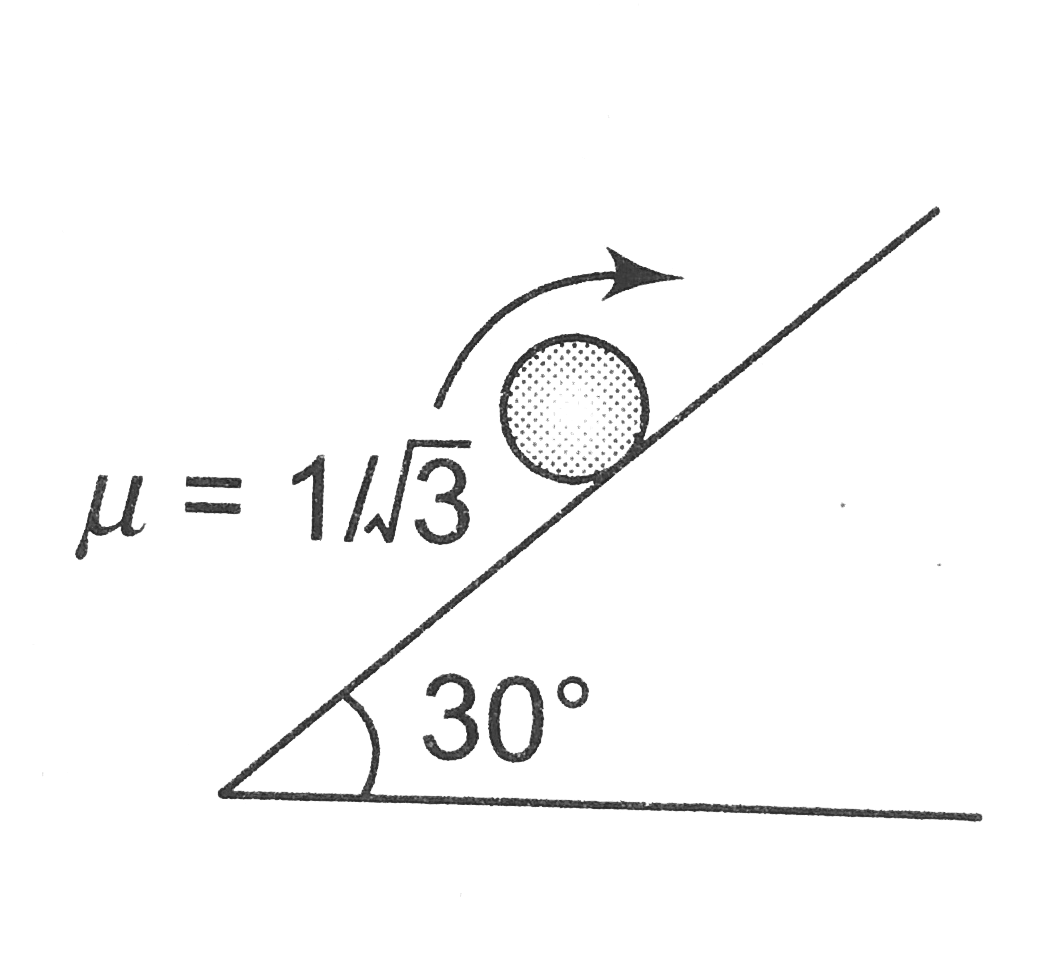 .
.
View SolutionA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
View Solution
