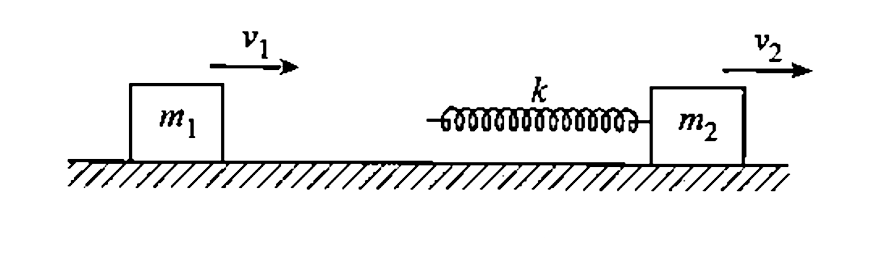
A block of mass m1 =2 kg slides along a firictionless table with a speed of 10m/s. Directly infront of it,and moving in the same direction is a block of mass m2 5 kg moving at 3 m/s. A mass less spring with a spring constant 11.2 N/cm is attached to as shown in figure-5.146. When the block collide,what is the maximum compression of the spring ? Assume that the spring does not bend.
The correct Answer is:[0.25 m]
Step by step video, text & image solution for A block of mass m_(1) =2 kg slides along a firictionless table with a speed of 10m//s. Directly infront of it,and moving in the same direction is a block of mass m_(2) 5 kg moving at 3 m//s. A mass less spring with a spring constant 11.2 N//cm is attached to as shown in figure-5.146. When the block collide,what is the maximum compression of the spring ? Assume that the spring does not bend. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - MCQ16videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
A block of mass 2kg slides on a frictionless table with with a speed of 10ms−1. Directly in front of it and moving in the same direction is a block of mass 5 kg moving at 3ms−1. A massless spring with force constant k=1120Nm−1 is attached to its back (the side facing 2 kg mass) When the blocks collide, what is the maximum compression of the spring ?
[Hint : Apply 'work energy' theorem to the system of block and principle of conservation of momentum]View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
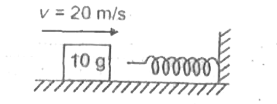 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43m - Question 2 - Select One
A block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
A2×10−2mB0.2mC20mD200m - Question 3 - Select One
Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
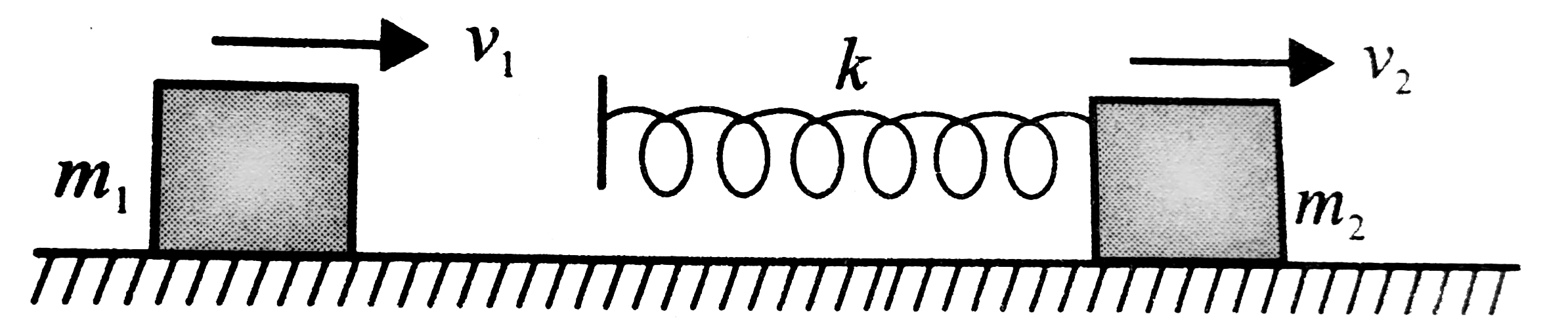 A0.06mB0.04mC0.02mDnone of these
A0.06mB0.04mC0.02mDnone of these
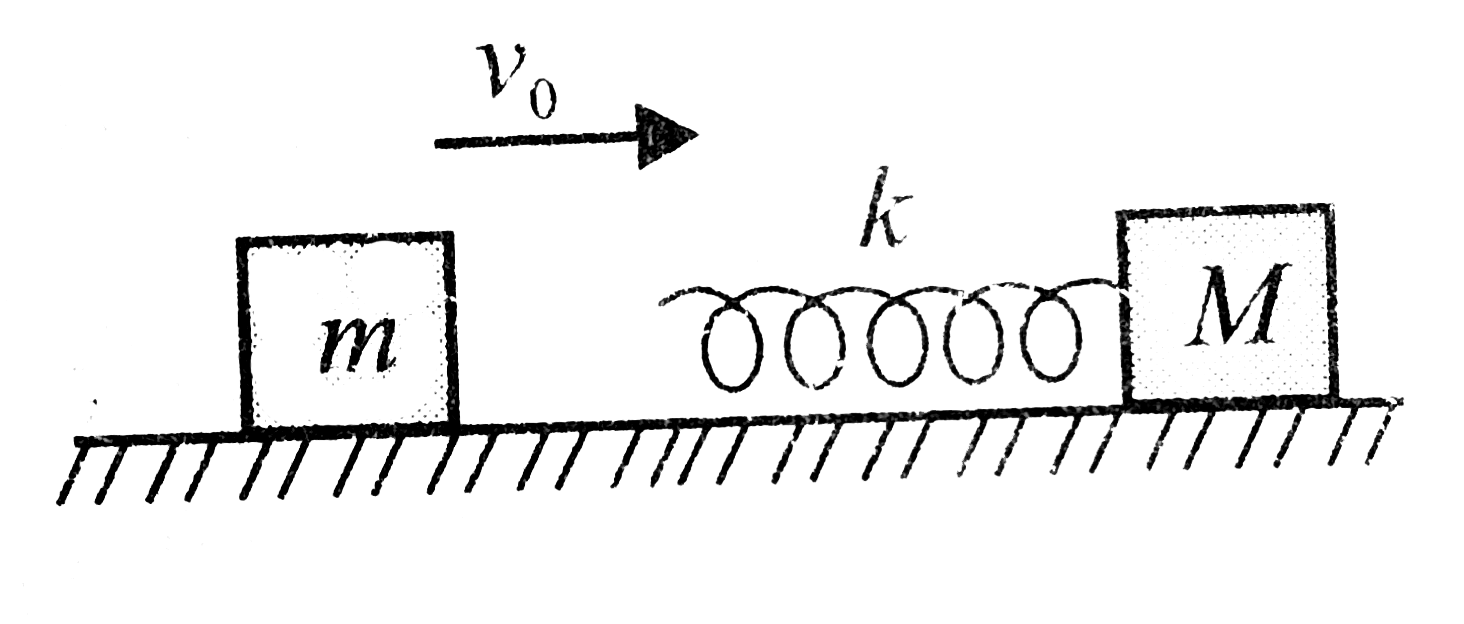
A block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionTwo blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
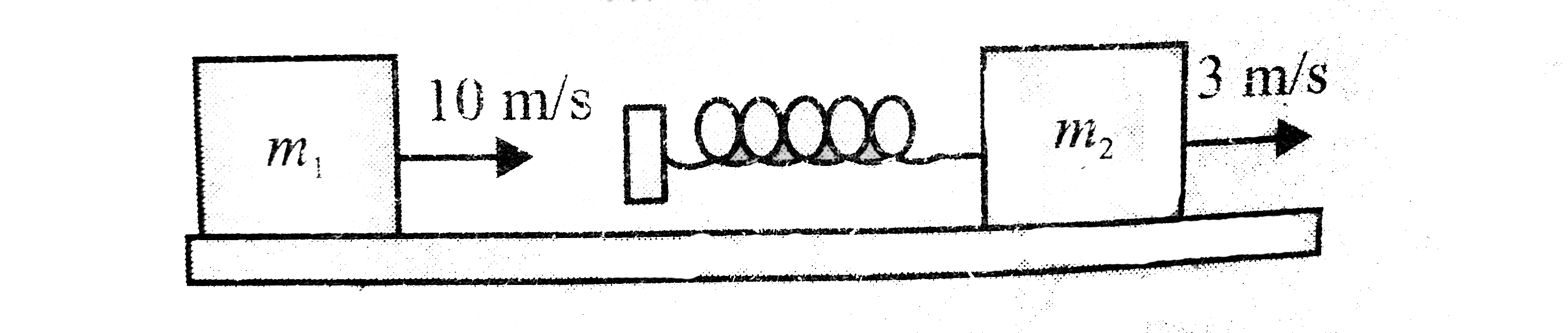 View Solution
View SolutionA block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
 View Solution
View SolutionTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
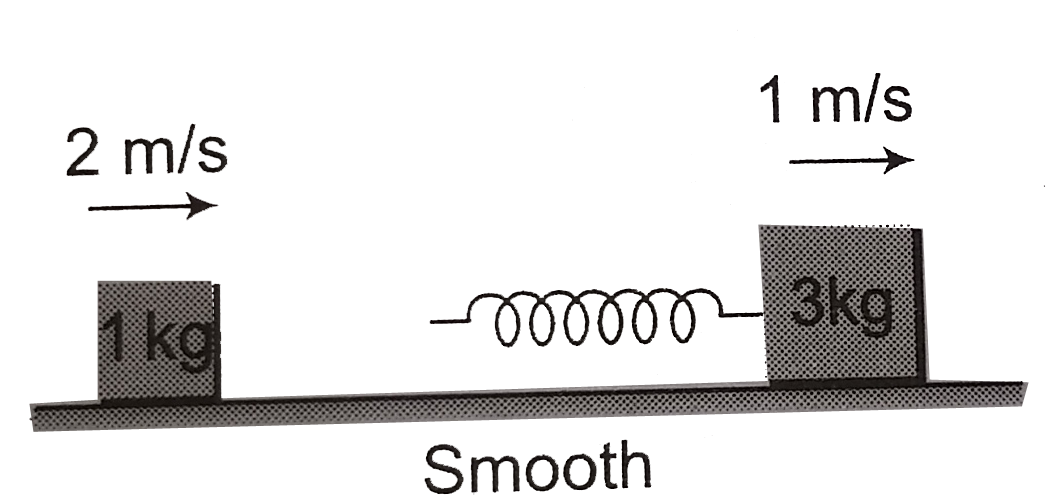 View Solution
View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
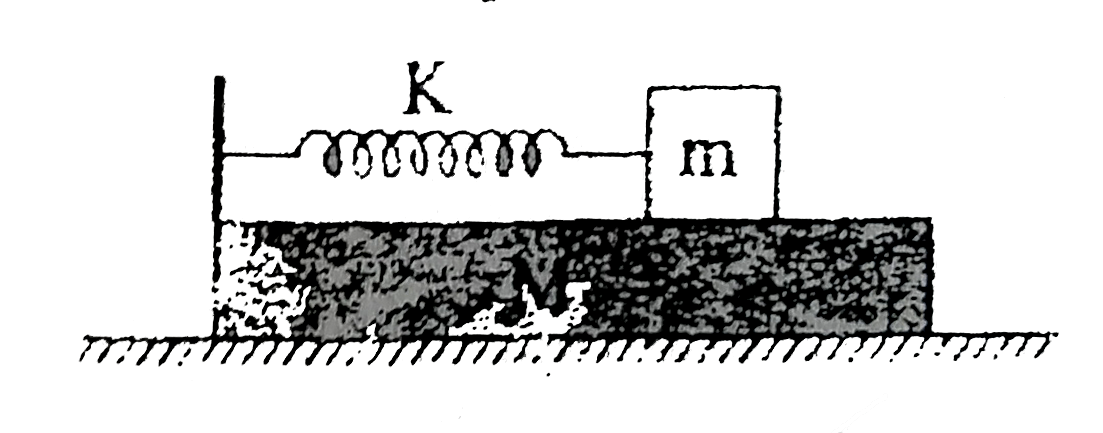 View Solution
View Solution

