The interface of two liauids of densities ρ and 2ρ respectively lies at the point A in a U tube at rest. The height of liquid columb above A is 8a/3 where AB = a. The cross-sectional area of the tube is S. With what angular velocity the tube must be whirled about a vertical axis at a distance 'a' such that the interface of the liquids shifts towards B by 2a/3.
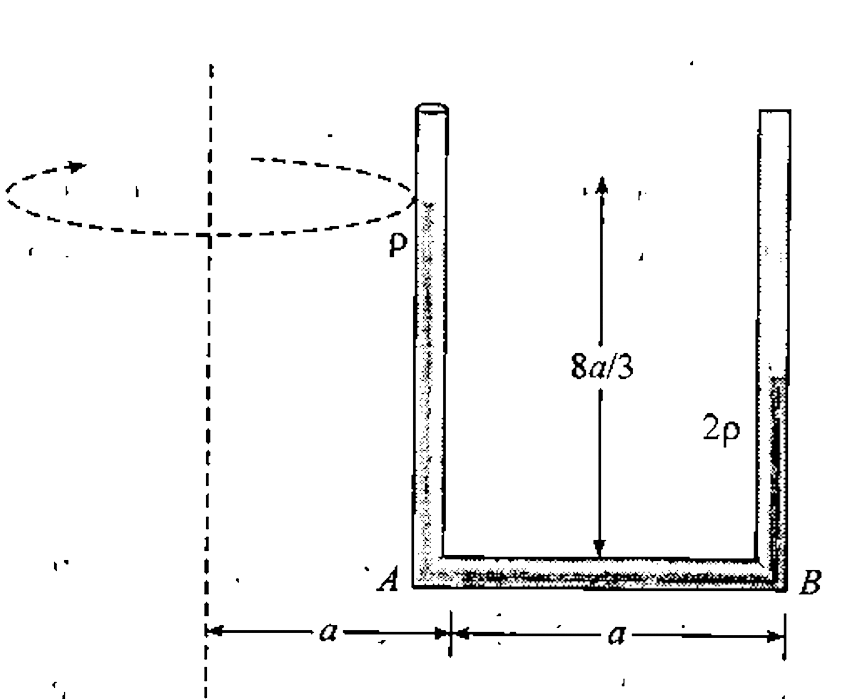
The correct Answer is:[√18g19a]
Topper's Solved these Questions
Similar Questions
A liquid of density ρ and surface tension S rises to a height h in a capillary tube of diameter D. what is the weight of the liquid in the capillary tube? Angle of contact is 0∘.
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
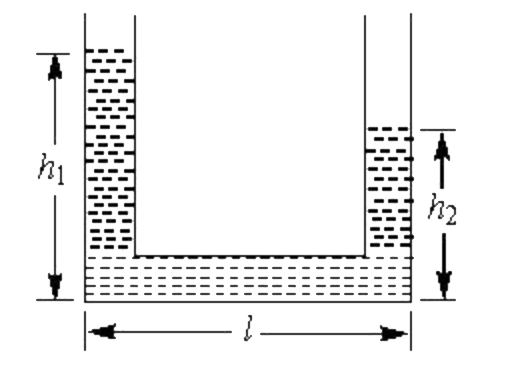
View Solution
Knowledge Check
A liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
 Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards left
Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards leftIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
 A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of theseIn the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.
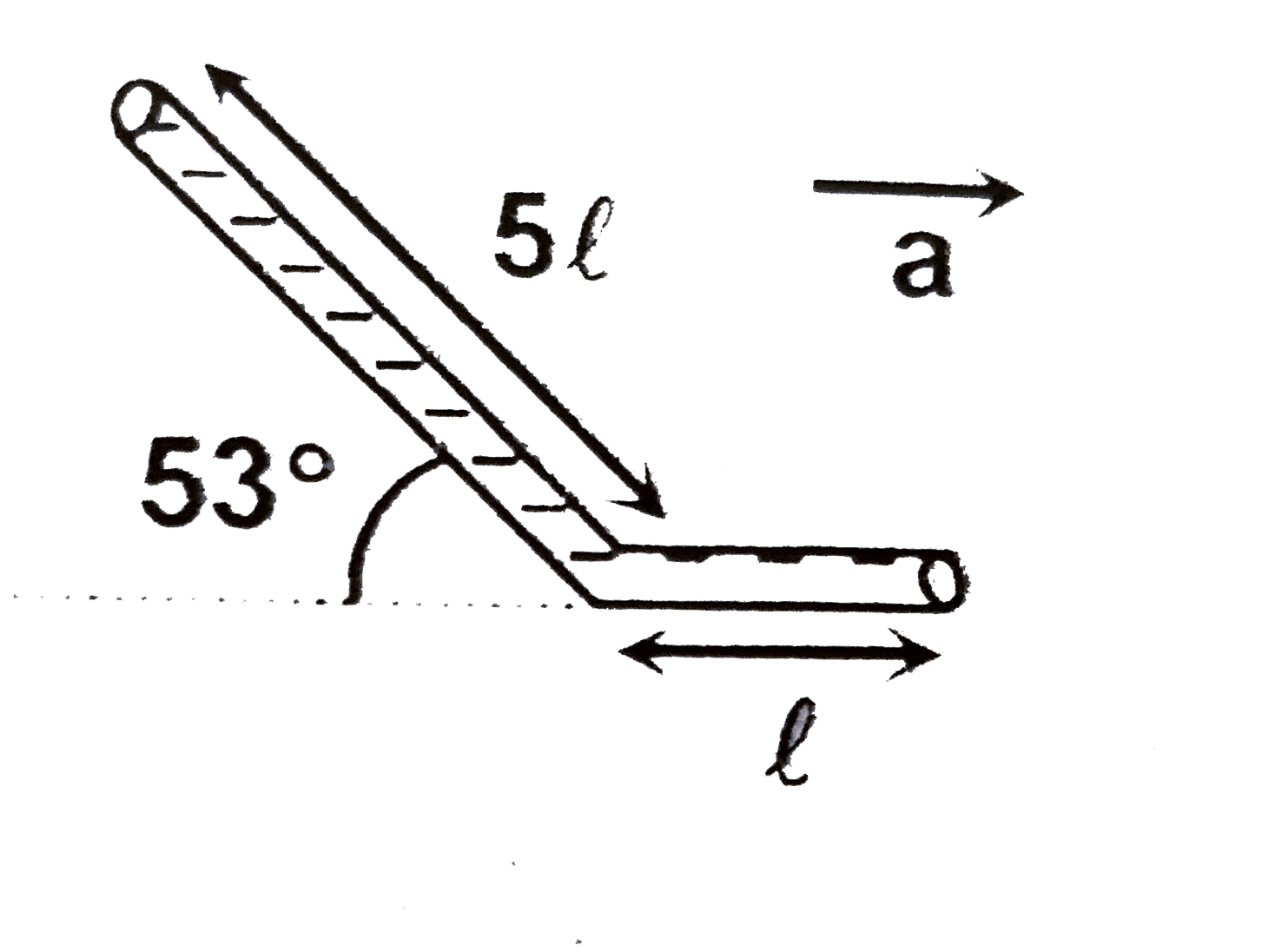 A35gB45gCgD4g
A35gB45gCgD4g
A U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
View SolutionA U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View SolutionIn the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.

View SolutionThree liquids having densities ρ1,ρ2,ρ3 are filled in a U-tube. Length of each liquid column is equal to I, ρ1>ρ2>ρ3 and liquids remain at rest (relative to the tube) in the position shown in the figure. It is possible that

View Solution
