The rate of volume of flow of water (V) through a canal is found to be a function of the area of cross section A of the canal and velocity of water v. Show that the rate of volume flow is proportional to the velocity of flow of water.
Step by step video & image solution for The rate of volume of flow of water (V) through a canal is found to be a function of the area of cross section A of the canal and velocity of water v. Show that the rate of volume flow is proportional to the velocity of flow of water. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - PHYSICAL WORLD AND MEASUREMENTSEXERCISE - problem10videos
PHYSICAL WORLD AND MEASUREMENTS
- BOOK - SL ARORACHAPTER - PHYSICAL WORLD AND MEASUREMENTSEXERCISE - problem for self practice64videos
PHYSICAL WORLD AND MEASUREMENTS
- BOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise49videos
Physical world
- BOOK - SL ARORACHAPTER - PROJECTILE MOTIONEXERCISE - Problem For Self Practice50videos
PROJECTILE MOTION
Similar Questions
The rate of volume flow of water through a canal is found to be a function of the area of cross-section of the canal and velocity of water. Show that the rate of volume flow is proportional to the velocity of flow of water.
View SolutionThe rate of flow of water through a horizontal pipe of changing cross section is 100 litres per hour. Calculate the velocity of water flow at a point where diameter of the tube is 4 cm?
View Solution
Knowledge Check
- Question 1 - Select One
When water is flowing through a pipe with a speed v, then its power is proportional to
Av2Bv3/2Cv3D√v - Question 2 - Select One
Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, ρ being the density of water?
Ap+2ρv2Bp−2ρv2Cp+32ρv2Dp−32ρv2 - Question 3 - Select One
If water falls from a tap, then the volume rate of flow of water at depth of h, (A0 is the area of cross-section of the mouth and A02 is the corresponding area at depth h)
AA0√2ghBA0√23ghC2A0√ghDA0√3gh
Water flows through a horizontal pipe of varying area of cross-section at the rate of 10 cubic metre per minute. Determine the velocity of water at a point where radius of pipe is 10cm.
View SolutionWater flows through a horizontal pipe of varying cross-section at the rate of 20 litres per minuts , determine the velocity of water at a point where diameter is 4cm
View SolutionWater flows out of a wide vessel through a small orifice. Express the flow velocity as a function of the height of the column of liquid.
View SolutionThe velocity of the water flowing from the inlet pipe is less than the velocity of water flowing out from the spin pipe B. Then
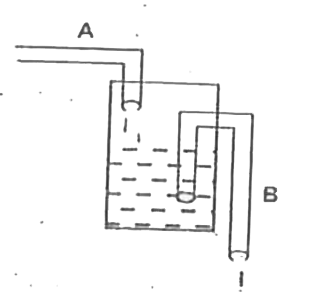 View Solution
View SolutionA water tank has a hole in its wall at a distance of 40 m below the free surface of water. Compute the velocity of flow of water from the hole. If the radius of the hole is 1 mm. find the rate of flow of water
View Solution

