A rod revlving 60 times in a minute about an axis passing through an end at right angles to the length, has kinetic energy of 400 J. find the moment of inertia of the rod.
The correct Answer is:20.26kgm2
To find the moment of inertia of the rod, we can follow these steps:
Step 1: Convert the rotational speed from revolutions per minute to radians per second.
The rod is revolving at 60 revolutions per minute (rpm). To convert this to radians per second (rad/s), we use the following conversion:
ω=revolutions per minute×2π radians1 revolution×1 minute60 seconds
Substituting the values:
ω=60×2π60=2π rad/s
Step 2: Use the formula for rotational kinetic energy.
The formula for rotational kinetic energy (KE) is given by:
KE=12Iω2
Where:
- KE is the kinetic energy (400 J)
- I is the moment of inertia (which we need to find)
- ω is the angular velocity (which we calculated as 2π rad/s)
Step 3: Substitute the known values into the kinetic energy formula.
We can rearrange the formula to solve for I:
400=12I(2π)2
Step 4: Simplify the equation.
First, calculate (2π)2:
(2π)2=4π2
Now substitute this back into the equation:
400=12I(4π2)
This simplifies to:
400=2π2I
Step 5: Solve for the moment of inertia I.
Rearranging gives:
I=4002π2=200π2
Step 6: Calculate the numerical value of I.
Using π≈3.14:
I≈200(3.14)2≈2009.8596≈20.26 kg m2
Final Answer:
The moment of inertia of the rod is approximately 20.26kg m2.
---
The rod is revolving at 60 revolutions per minute (rpm). To convert this to radians per second (rad/s), we use the following conversion:
The formula for rotational kinetic energy (KE) is given by:
- KE is the kinetic energy (400 J)
- I is the moment of inertia (which we need to find)
- ω is the angular velocity (which we calculated as 2π rad/s)
We can rearrange the formula to solve for I:
First, calculate (2π)2:
Rearranging gives:
Using π≈3.14:
The moment of inertia of the rod is approximately 20.26kg m2.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem24videos
ROTATIONAL MOTION
- BOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions97videos
PROPERTIES OF SOLIDS
- BOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE353videos
System of particles & rotational Motion
Similar Questions
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionCalculate the moment of inertia of a rectangular frame formed by uniform rods having mass m each as shown in about an axis passing through its centre and perpendicular to the plane of frame. Also find moment of inertia about an axis passing through PQ ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows the variation of the moment of inertia of a uniform rod, about an axis passing through itss centre and inclined at an angle θ to the length. The moment of inertia of the rod about an axis passing through one of its ends and making an angle θ=π3 will be
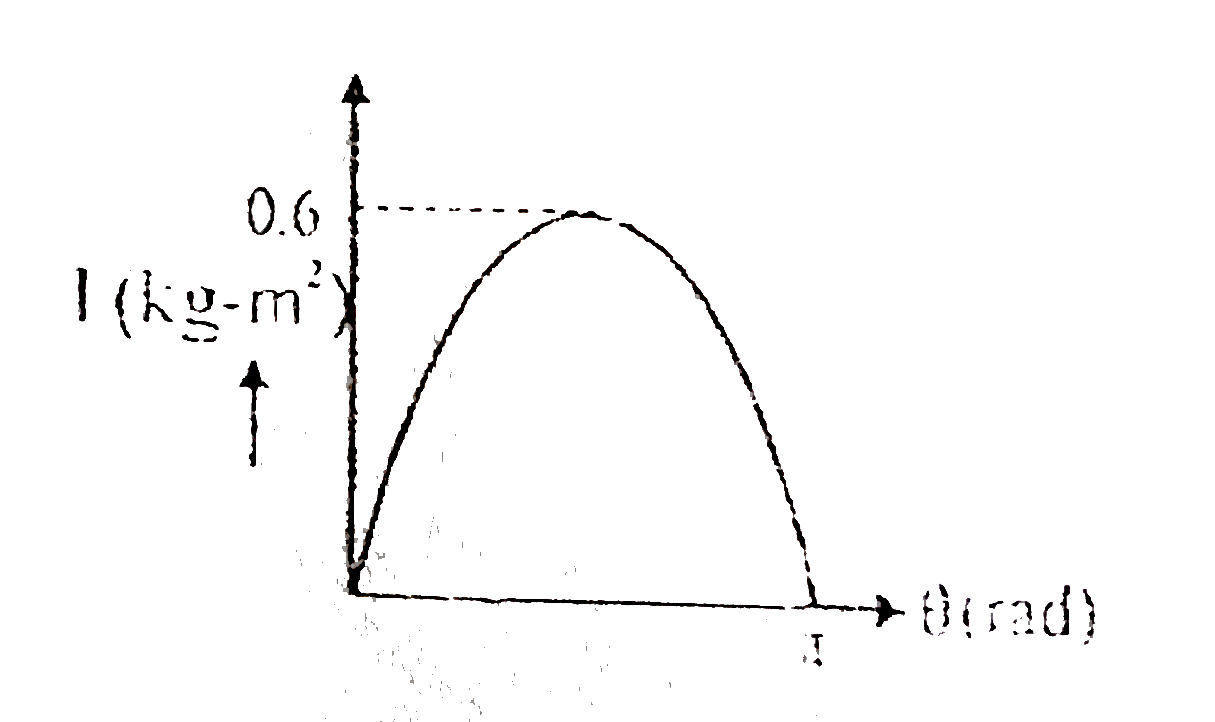 A0.45kg−m2B1.8kg−m2C2.4kg−m2D1.5kg−m2
A0.45kg−m2B1.8kg−m2C2.4kg−m2D1.5kg−m2 - Question 2 - Select One
The moment of inertia of a circular ring about an axis passing through its diameter is I . This ring is cut then unfolded into a uniform straight rod. The moment of inertia of the rod about an axis perpendicular to its length passing through one of its ends is
A4π2I3B8π2I3C16π2I3D2π2I3 - Question 3 - Select One
Three identical uniform thin metal rods form the three sides of an equilateral triangle. If the moment of inertia of the system of these three rods about an axis passing through the centroid of the triangle and perpendicular to the plane of the triangle is 'n' times the moment of inertia of one rod separately about an axis passing through the centre of the rod and perpendicular to its length, the value of 'n' is
A3B6C9D12
Moment of inertia of a thin uniform rod about an axis passing through one end perpendicular to its length is I . Then moment of inertia the same rod about the central axis perpendicular to its plane is
View SolutionA rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0 . Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
View SolutionIf l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View Solution

