In an experiment using the Cavendish balance, the smaller spheres have a mass of 5.0×10−3kg each, the larger spheres have a mass 12.0 kg each, the length of the rod is 100.0 cm, the torsion constant of the fibre is 3.56×10−8 Nm per rad, the angle of twist is 4.86×10−3rad, and the distance between the centres of each pair of heavy and light spheres is 15.0 cm. Compute the value of the gravitational constant G from this data.
Step by step video & image solution for In an experiment using the Cavendish balance, the smaller spheres have a mass of 5.0xx10^(-3)kg each, the larger spheres have a mass 12.0 kg each, the length of the rod is 100.0 cm, the torsion constant of the fibre is 3.56xx10^(-8) Nm per rad, the angle of twist is 4.86xx10^(-3)rad, and the distance between the centres of each pair of heavy and light spheres is 15.0 cm. Compute the value of the gravitational constant G from this data. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - GRAVITATIONEXERCISE - Problem From Competitive Examinations14videos
GRAVITATION
- BOOK - SL ARORACHAPTER - GRAVITATIONEXERCISE - Exercise480videos
GRAVITATION
- BOOK - SL ARORACHAPTER - FLUIDS IN MOTIONEXERCISE - All Questions117videos
FLUIDS IN MOTION
- BOOK - SL ARORACHAPTER - HEATEXERCISE - Problem For Self Practice72videos
HEAT
Similar Questions
In an experiment using the Cavendish balance , the smaller spheres have a mass of 20 kg each , the larger spheres have a mass 5 kg each , the length of the rod is 50.0 cm the torsion constant of the fibre is 4.8×10−8 Nm per radian , the angle of twist is 7×10−3 rad , and the distance between the centres of each pair of heavy and light spheres is 100 cm . Compute the value of the gravitational constant G from this data .
View SolutionTwo spheres of uniform density have masses 10 kg and 40 kg. The distance between the centres of the spheres is 200 m. Find the gravitatioanl force between them.
View Solution
Knowledge Check
- Question 1 - Select One
Two spheres, each of mass 625 kg, are placed with their centres 50 cm apart. The gravitational force between them is
A10.42 dyneB15.42 dyneC20.42 dyneD5.42 dyne
The balance wheel of a watch has a moment of inertia of 2×10−8kgm2 and the torsional constant of its hair spring is 9.8×10−8 Nm rad−1 calculate its frequency.
View SolutionCalculate the force of attraction between two balls each of mass 10kg when their centres are 10 cm apart. The value of gravitational constant G=6.67×10−11Nm2kg−2
View SolutionA sphere of mass 40kg is attracted by a second sphere of mass 15kg, when their centres are 20cm apart, with a force of 0.1 miligram weight. Caculate the value of gravitational constant.
View SolutionThe masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100m, find the magnitude of the gravitational force between them.
View SolutionThe masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100 m, find the magnitude of the gravitational force between them.
View SolutionIn Cavendish's experiment, let each small mass be 20g and each large mass be 5kg. The rod connecting the small masses is 50cm long, while the small and the large spheres are separated by 10.0cm. The torsion constant is 4.8×10−8kgm2s−2 and the resulting angular deflection is 0.4∘. Calculate the value of universal gravitational constant G from this data.
View SolutionTwo identical, small, charged spheres, each having a mass of 4.0×10−2kg hang in equilibrium as shown in Fig. 22-10a. The length of each string is 1.5m and the angle θ is 37.0∘. Find the magnitude of the charge on each sphere.
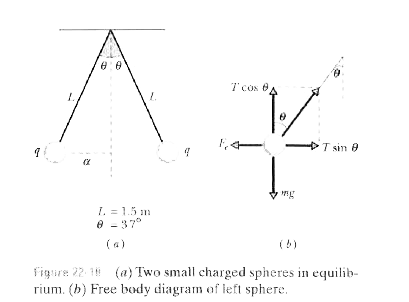 View Solution
View Solution

