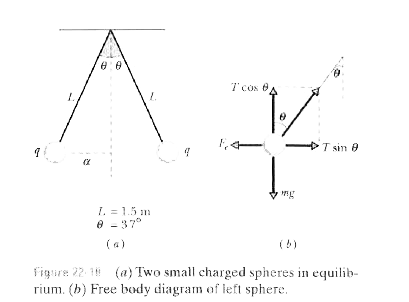
Two identical, small, charged spheres, each having a mass of 4.0×10−2kg hang in equilibrium as shown in Fig. 22-10a. The length of each string is 1.5m and the angle θ is 37.0∘. Find the magnitude of the charge on each sphere.
KEY IDEA
From Fig. 22-10a, we can see that the two spheres exert repulsive forces on each other. If they are held close to each other and released, they will move outward from the center and settle into the configuration in Fig. 22-10a after the damped oscillations due to air resistance have vanished.
The key phrase "in equilibrium" helps us to classify this as an equilibrium problem, which we approach as we did equilibrium problems in the chapter on Newton.s Laws in (Volume 1) with the added feature that one of the forces on a sphere is an electric force. We analyze this problem by drawing the free-body diagram for the left-hand sphere in Fig. 22-10b. The sphere is in equilibrium under the application of forces T from the string, the electric force Fe from the other sphere, and the gravitational force mg.
Calculations: Because the sphere is in equilibrium, the forces in the horizontal and vertical directions must separately add up to zero.
∑Fx=Tsinθ−Fe (22−11)
∑Fy=Tcosθ−mg (22−12)
Frow Eq. 22-12, we see that T=mg/cosθ, thus, T can be eliminated from Eq. 22-11 if we make this substitution. This gives a value for the magnitude of the electric force Fe:
Fe=mgtanθ=(4×10−2kg)(10m/s2)tan37∘=0.3N.
Considering the geometry of the triangle in Fig. 22-10a, we see that sinθ=α/L. Therefore,
a=Lsinθ=(1.5m)sin37∘=0.9m
The separation of the spheres is 2a=1.8m. From Coulomb.s law (Eq. 22-10), the magnitude of the electric froce is
Fe=ke|q|2r2
where r = 2a = 1.8m and |q| is the magnitude of the charge on each sphere. This equation can be solved for |q|2 to give
|q|2=F3r2ke=0.3×(1.8)29×109Nm2/C2=1.08×10−10C2
|q|=6√3μC
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
Two identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
View SolutionTwo identical small charged spheres, each having a mass m, hang in equilibrium the length of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
View Solution
Knowledge Check
Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
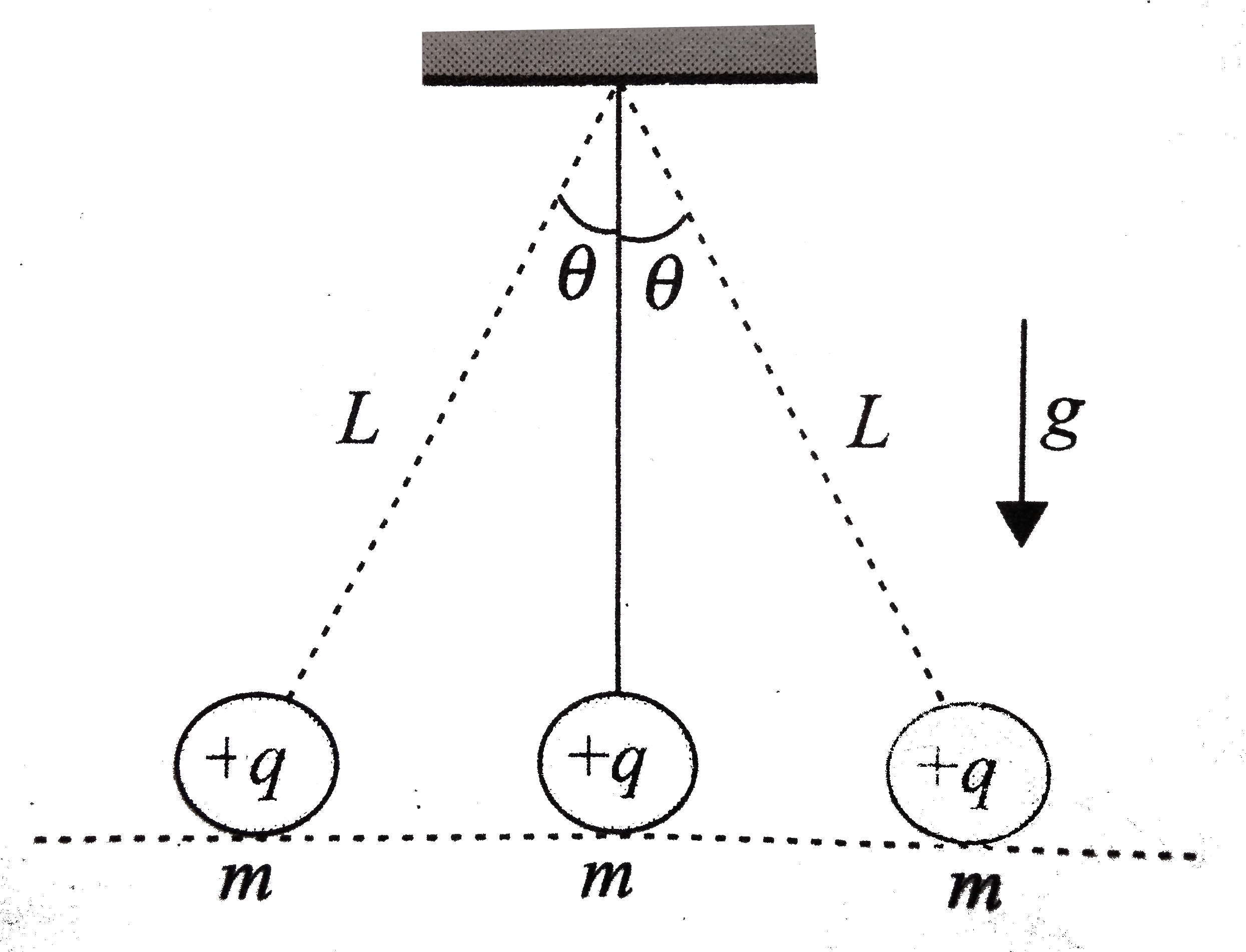 Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of these
Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of these
Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is

View SolutionA small object is suspended at rest from two strings as shown in fig. The magnitude of the force exerted by each string on the object is 10√2N. Find the magnitude of the mass of the object.

View SolutionA small object is suspended at rest from two strings as shown in fig. The magnitude of the force exerted by each string on the object is 10√2N. Find the magnitude of the mass of the object.

View SolutionTwo identical particles, each having a charge of 2.0×10−4C and mass of 10g, are kept at a separation of 10cm and then released. What would be the speeds of the particles when the separation becomes large?
View SolutionIn an experiment using the Cavendish balance , the smaller spheres have a mass of 20 kg each , the larger spheres have a mass 5 kg each , the length of the rod is 50.0 cm the torsion constant of the fibre is 4.8×10−8 Nm per radian , the angle of twist is 7×10−3 rad , and the distance between the centres of each pair of heavy and light spheres is 100 cm . Compute the value of the gravitational constant G from this data .
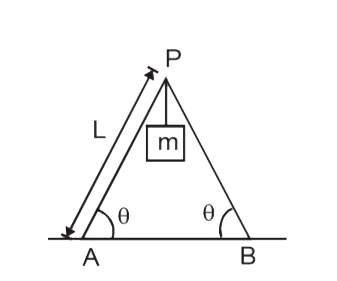
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View Solution
