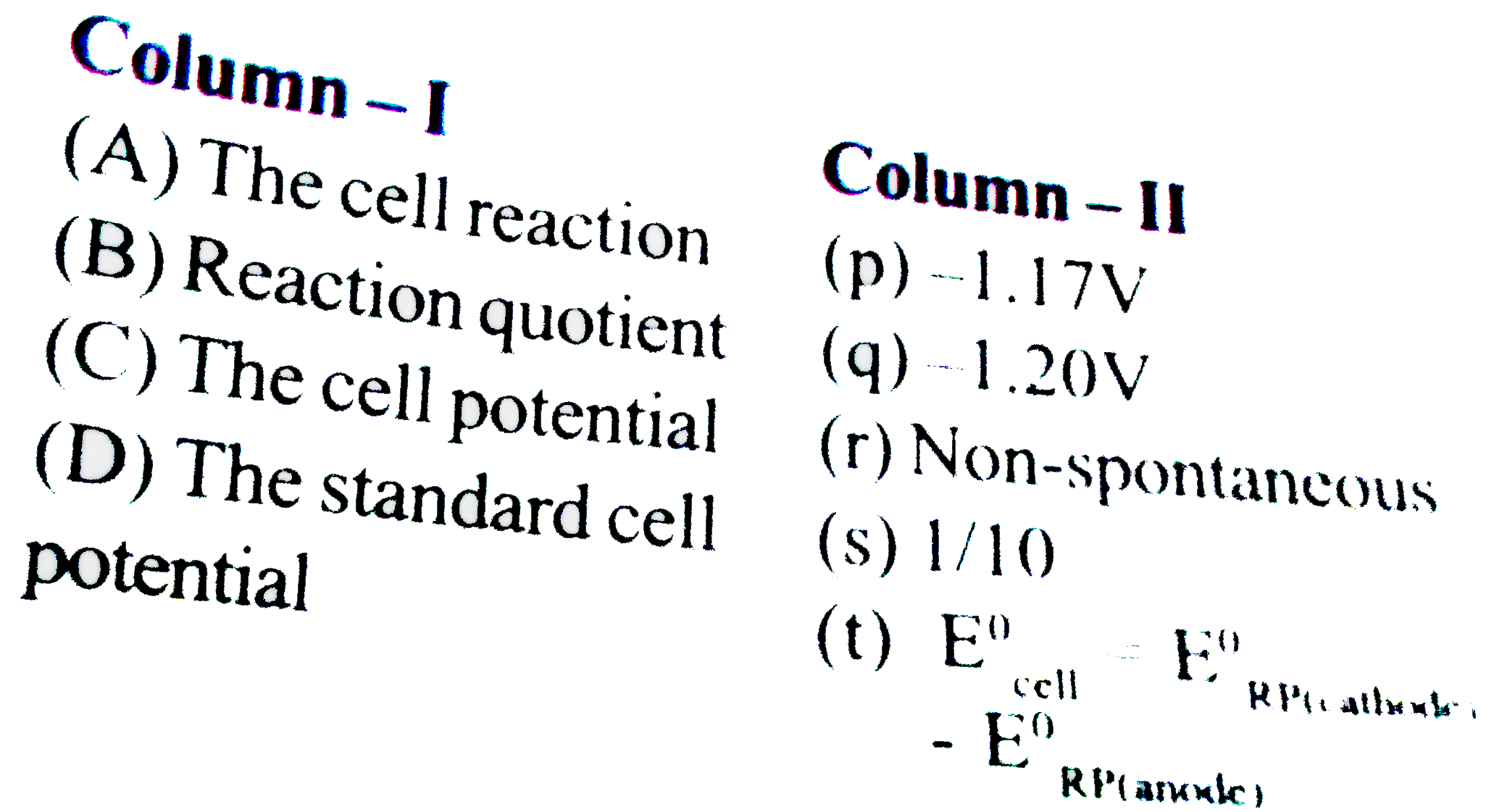Given the cell: Cd(s)∣∣Cd(OH)2(s)∣∣NaOH(aq,0.01M)|H2(g,1bar)|Pt(s)
with Ecell=0.0V.ifE∘Cd2+∣Cd=−0.39V,thenKspofCd(OH2)is:
0.1
10−13
10−15
None of these
The correct Answer is:C
To solve the problem, we need to determine the solubility product constant (Ksp) of cadmium hydroxide (Cd(OH)₂) based on the given electrochemical cell and the provided data.
1. Identify the half-reactions:
- The oxidation half-reaction involves cadmium (Cd) converting to cadmium ions (Cd²⁺):
Cd(s)→Cd2+(aq)+2e−
- The reduction half-reaction involves hydrogen ions (H⁺) converting to hydrogen gas (H₂):
2H+(aq)+2e−→H2(g)
2. Overall cell reaction:
Combining the half-reactions gives the overall cell reaction:
Cd(s)+2H+(aq)→Cd2+(aq)+H2(g)
3. Use the Nernst equation:
The Nernst equation relates the cell potential to the concentrations of the reactants and products:
Ecell=E∘cell−0.059nlogQ
Where:
- Ecell=0.0V
- E∘cell=E∘cathode−E∘anode=0−(−0.39)=0.39V
- n=2 (number of electrons transferred)
4. Calculate the reaction quotient (Q):
The reaction quotient Q for the overall reaction is given by:
Q=(Cd2+)(H+)2
Given that the concentration of OH− is 0.01M, we can find the concentration of H+ using the ion product of water:
Kw=(H+)(OH−)=10−14
Therefore:
(H+)=10−140.01=10−12M
5. Substituting values into the Nernst equation:
Rearranging the Nernst equation:
0=0.39−0.0592log((Cd2+)(10−12)2)
Simplifying gives:
0.39=0.0592log((Cd2+)10−24)
6. Solving for (Cd2+):
Rearranging gives:
log((Cd2+))=0.39×20.059+24
Calculating the left side:
log((Cd2+))=13.23+24=37.23
Therefore:
(Cd2+)=10−37.23≈5.88×10−38M
7. Calculate Ksp:
The dissociation of cadmium hydroxide is:
Cd(OH)2⇌Cd2++2OH−
Thus:
Ksp=(Cd2+)(OH−)2
Substituting the values:
Ksp=(5.88×10−38)(0.01)2=5.88×10−38×10−4=5.88×10−42
Final Answer:
The Ksp of Cd(OH)₂ is approximately 5.88×10−42.
- The oxidation half-reaction involves cadmium (Cd) converting to cadmium ions (Cd²⁺):
Cd(s)→Cd2+(aq)+2e−
- The reduction half-reaction involves hydrogen ions (H⁺) converting to hydrogen gas (H₂):
2H+(aq)+2e−→H2(g)
Combining the half-reactions gives the overall cell reaction:
Cd(s)+2H+(aq)→Cd2+(aq)+H2(g)
The Nernst equation relates the cell potential to the concentrations of the reactants and products:
Ecell=E∘cell−0.059nlogQ
Where:
- Ecell=0.0V
- E∘cell=E∘cathode−E∘anode=0−(−0.39)=0.39V
- n=2 (number of electrons transferred)
The reaction quotient Q for the overall reaction is given by:
Q=(Cd2+)(H+)2
Given that the concentration of OH− is 0.01M, we can find the concentration of H+ using the ion product of water:
Kw=(H+)(OH−)=10−14
Therefore:
(H+)=10−140.01=10−12M
Rearranging the Nernst equation:
0=0.39−0.0592log((Cd2+)(10−12)2)
Simplifying gives:
0.39=0.0592log((Cd2+)10−24)
Rearranging gives:
log((Cd2+))=0.39×20.059+24
Calculating the left side:
log((Cd2+))=13.23+24=37.23
Therefore:
(Cd2+)=10−37.23≈5.88×10−38M
The dissociation of cadmium hydroxide is:
Cd(OH)2⇌Cd2++2OH−
Thus:
Ksp=(Cd2+)(OH−)2
Substituting the values:
Ksp=(5.88×10−38)(0.01)2=5.88×10−38×10−4=5.88×10−42
The Ksp of Cd(OH)₂ is approximately 5.88×10−42.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - ELECTROCHEMISTRYEXERCISE - Level 1 (Q.1 To Q.30)1videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - ELECTROCHEMISTRYEXERCISE - Level 1 (Q.91 To Q.120)1videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - DILUTE SOLUTIONEXERCISE - Level 3 - Match The Column1videos
DILUTE SOLUTION
- BOOK - NARENDRA AWASTHICHAPTER - GASEOUS STATEEXERCISE - Level 3 - Subjective Problems1videos
GASEOUS STATE
Similar Questions
Knowledge Check
- Question 1 - Select One
The standard emf of the cell,
Cd(s)∣∣CdCI2(aq)(0.1M)∣∣∣∣AgCI(aq)∣∣Ag(s)
in which the cell reaction
Cd(s)+2AgCI(s)→2Ag(s)+Cd2+(aq)+2CI−(aq) is 0.6915 V at 0 ∘C and 0.6573 V at 25 ∘C . The enthalpy change of the reaction at 25 ∘C isA+48.179 KJB-205.5 KJC+123.5 KJD-167.26 KJ
Calculate the emf of the following cell at 25∘ C
Zn∣∣Zn2+(0.001M)∣∣∣∣H+(0.01M)∣∣H2(g)(1¯)∣Pt(s)
E∘Zn2+/Zn=−0.76V,E∘H+/H2=0.00VView SolutionCalculate the cell e.m.f. and ΔG for the cell reaction at 298 K for the cell.
Zn(s)∣∣Zn2+(0.0004M)∣∣∣∣Cd2+(0.2M)∣∣Cd(s)
Given E∘Zn2+/Zn=−0.763V,E∘cd2+/cd=−0.403V at 298K,F=96500C mol−1.View SolutionCalculate the cell e.m.f. and ΔG for the cell reaction at 298K for the cell.
Zn(s)∣∣Zn2+(0.0004M)∣∣∣∣Cd2+(0.2M)∣∣Cd(s)
Given, E∘Zn2+/Zn=−0.763V,E∘Cd+2/Cd=−0.403V at 298K.
F=96500Cmol−1.View SolutionCalculate the cell emf and △rG∘ for the cell reactin at 25∘C
Zn(s)∣∣Zn2+(0.1M)∣∣∣∣Cd2+(0.01M)∣∣Cd(s)
(given E∘Zn2+/Zn=−0.763V,E∘Cd2+/Cd=−0.403V
1F=96500Cmol−1,R=8.314JK−1mol−1]View SolutionCalculate the standard cell potentials of the galvanic cells in which the following reactions take place.
(a) 2Cr(s)+3Cd2+→2Cd3+(aq)+3Cd(s)
Given E∘Cr3+/Cr=−0.74 V,E∘Cd2+/Cd=−0.40 V
(b) Fe2+(aq)+Ag+(aq)→Fe3+(aq)+Ag(s)
Gievn E∘Ag+/Ag=0.80 V,E∘Fe3+/Fe2+=0.77 V
Also calculate ΔG∘ and equilibrium constant for the reaction.View SolutionIf the equilibrium constant for the reaction Cd2+(aq)+4NH3(aq)⇔Cd(NH3)2+4(aq) is 10x then find the value of x.
(Given: E∘Cd2+|Cd=−0.4V,E∘Cd(NH3)2+4|Cd=−0.61V)View SolutionThe e.m.f. of the cell Cd(s)|CdCl2(0.1M)||AgCl(s)|Ag(s) in which the cell reaction is Cd(s)+2AgCl(s)→2Ag(s)+Cd2+(aq)+2Cl−(aq)
is 0.6915 V at 0∘C and 0.6753 at 25∘C. Calculate the enthalpy change of the reaction at 25∘C.View Solution