Effect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If statndard heat of dissociation of PCl5 is 230 cal then slope of the graph of log vs 1T is :
50
-50
10
none of these
The correct Answer is:B
Step by step video, text & image solution for Effect of temperature on the equilibrium process analysed by using the thermodynamics From the thermodynamics reaction DeltaG^(@)=-2.30RTlogk DeltaG^(@): Standing free energy change DeltaG^(@)=DeltaH^(@)-TDeltaS^(@)…(ii) DeltaH^(@) :Standard heat of the reaction gt From eqns.(i) and(ii) -2RTlogk=DeltaH^(@)=TDeltaS^(@) DeltaS^(@) : standard entropy change implies" "logK=-(DeltaH^(@))/(2.3RT)+(DeltaS^(@))/(2.3R) Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =(-DeltaH^(@))/(2.3R) amd y intercept =(DeltaS^(@))/(2.3R) If at temperature T_(1) equilibrium constant be k_(1) and at temperature T_(2)equilibrium constant be k_(2) then : implies" "logK_(1)=-(DeltaH^(@))/(2.3RT_(1))+(DeltaS^(@))/(2.3R)..(iv) implies" "logK_(2)=-(DeltaH^(@))/(2.3RT_(2))+(DeltaS^(@))/(2.3R)...(v) Substracting e.q (iv) from (v), we get from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction If statndard heat of dissociation of PCl_(5) is 230 cal then slope of the graph of log vs (1)/(T) is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 8
1 Videos
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 9
1 Videos
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 6
1 Videos
- F-BLOCK ELEMENTSBOOK - GRB PUBLICATIONCHAPTER - F-BLOCK ELEMENTSEXERCISE - Subjective type
7 Videos
- HYDROCARBON (ALIPHATIC)BOOK - GRB PUBLICATIONCHAPTER - HYDROCARBON (ALIPHATIC)EXERCISE - Previous years jee questions
28 Videos
Similar Questions
The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such cases dinKdT=EaRT2 should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
If Arrhenius constant and Ea (activation energy0 are assumed to be constant then which of the following graph will be correct
View SolutionIf an element can exist in several oxidation states, it is convenient to display the reduction potentials corresponding to the various half reactions in diagrammatic from, known as Latimer diagram. The Latimer diagram for chlorine in acid solution is
Cl−4+1.20V−−−−→ClO−3+1.60V−−−−→ClO−2+1.60V−−−−→
ClO−+1.67V−−−−→Cl2+1.36V−−−−→Cl−
In basic solution is :
ClO−4+0.37V−−−−→ClO−3+0.30V−−−−→ClO−2+0.68−−−→
ClO−+0.42V−−−−→Cl2+1.36−−−→Cl−. The standard potentials for two nonadjacent species can also be calculated by using the concept that ΔG∘ is an additive property but using potential is not an assitive property and ΔG∘=−nFx0, If a given oxidation state is a the next higher oxidation state disproportionation can occur. The reverse of relative stabilities of the oxidation state can also be understood by drawing a graph of ΔG∘/F against oxidation state, known as Frost diagram, Choosing the stability of zero oxidation state arbitrery as zero. The most stable oxidation state of a apecies lies lowest in the digram Disproportionation is spontaneous if the species lies above a straight line joining its two product species.
Which of the following couple have same value of potential at pH = 0 and pH = 14?
View SolutionIn the photoelectric effect the eletrons are emiited intantaneously from a given matal plate when it is irradiated with radiation of frequency equal to or greater then some minimum ferquency, is called the threshold frequency.According to Planck's idea, light may be considered to be made up discrete particles called photons.Each photon carries energy equal ti hv.When this photon cllides with the electron of the metal, the electron acquires energy of the emitted electron is given by :
hv=K.Emaximum+PE=12mu2+PE
If the incident rediation is of threshold frequency the electron will be emitted without any kinetic energy
i.e hv0
∴12mu2=hv−hv0
A plot of kinetic energy of the emitted electron versus frequency of the incident radiation yields a straight line given as :
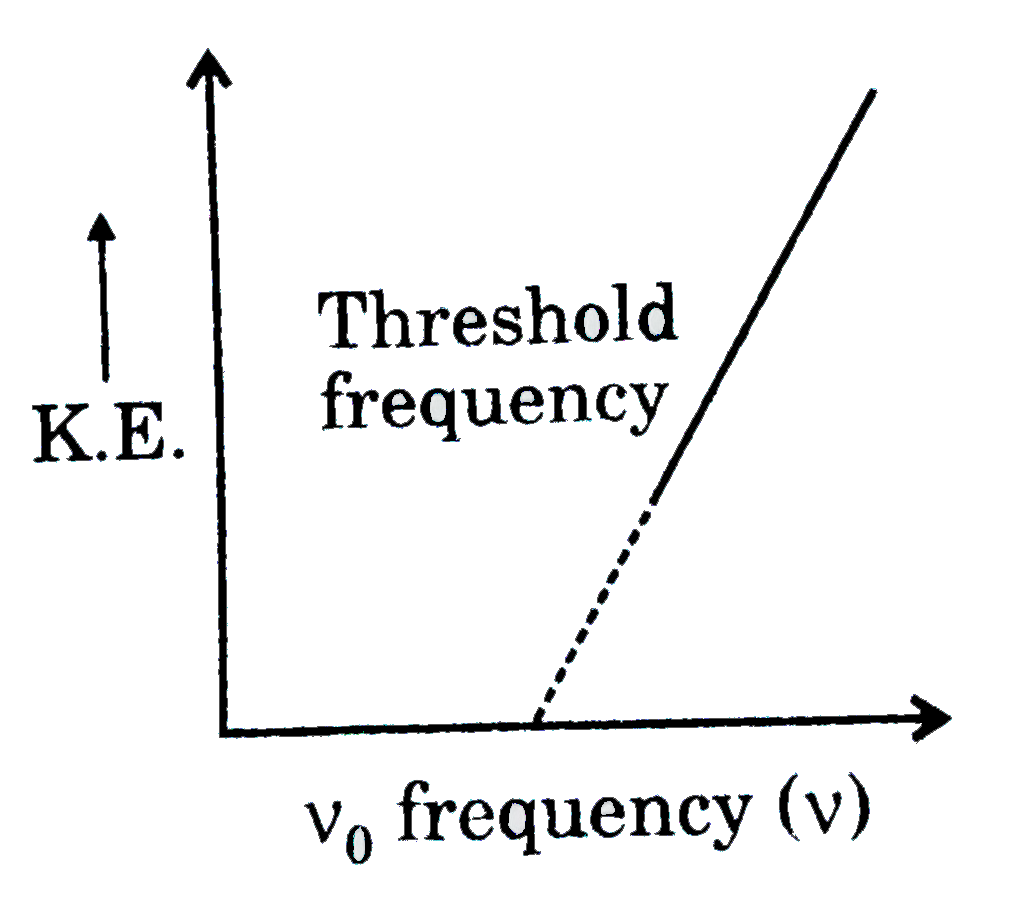
A beam of white light is dispersed into its wavelenght components of potassium metal. What of the electron emitted by the different light component ?
View SolutionThe first f-block organometallic compound [ThH(OR)(C5Me5)2] was prepared in late 1970s. Find the oxidation state of central metal atom/cation.
View SolutionWhich of the following will decolourise alkaline KMnO4?
View SolutionΔG=ΔH−TΔS and ltBRgt ΔG=ΔH+T[d(ΔG)dT]p, then(dEcelldT) is
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If for a particular reversible reaction
KC=57 abd 355∘C and KC=69 at 450∘C then
View SolutionThe relation ΔG=ΔH−TΔS was given by
View Solutionसमीकरण ΔG=ΔH−TΔS की व्युत्पत्ति कीजिए ।
View SolutionFor a process at a particular temperature and pressure, DeltaG=DeltaH-TDeltaS . It can be written as: -DeltaG=T[-(DeltaH)/(T)+DeltaS] . What does the quantity within the bracket indicate?
View SolutionIf DeltaG=DeltaH-TDeltaS and DeltaG = DeltaH+T[(d(DeltaG))/(dT)] , then variation EMF of a cell E, with temperature T, is given by
View SolutionThe relation ΔG=ΔH−TΔS was given by
View SolutionΔG=ΔH−TδSandΔG=ΔH+T[d(ΔG)dT] then (dEcelldT) is
View SolutionEstablish DeltaG = DeltaH- TDeltaS .
View Solution
