The electric field and the electric potential at a point are E and V respectively.
If V=0,E must be zero
If V≠0,E cannot be zero
If E≠0,V cannot be zero.
None of the these
The correct Answer is:A, B, D
Step by step video, text & image solution for The electric field and the electric potential at a point are E and V respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Figure shown three points A,B and C in a region of unifrom electric field →E. The line AB is perpendicular and BC is parallel to the field lines. Then which of the following holds good. Where VA,VB and VC represenet the electric potential at points A,B and C respectively
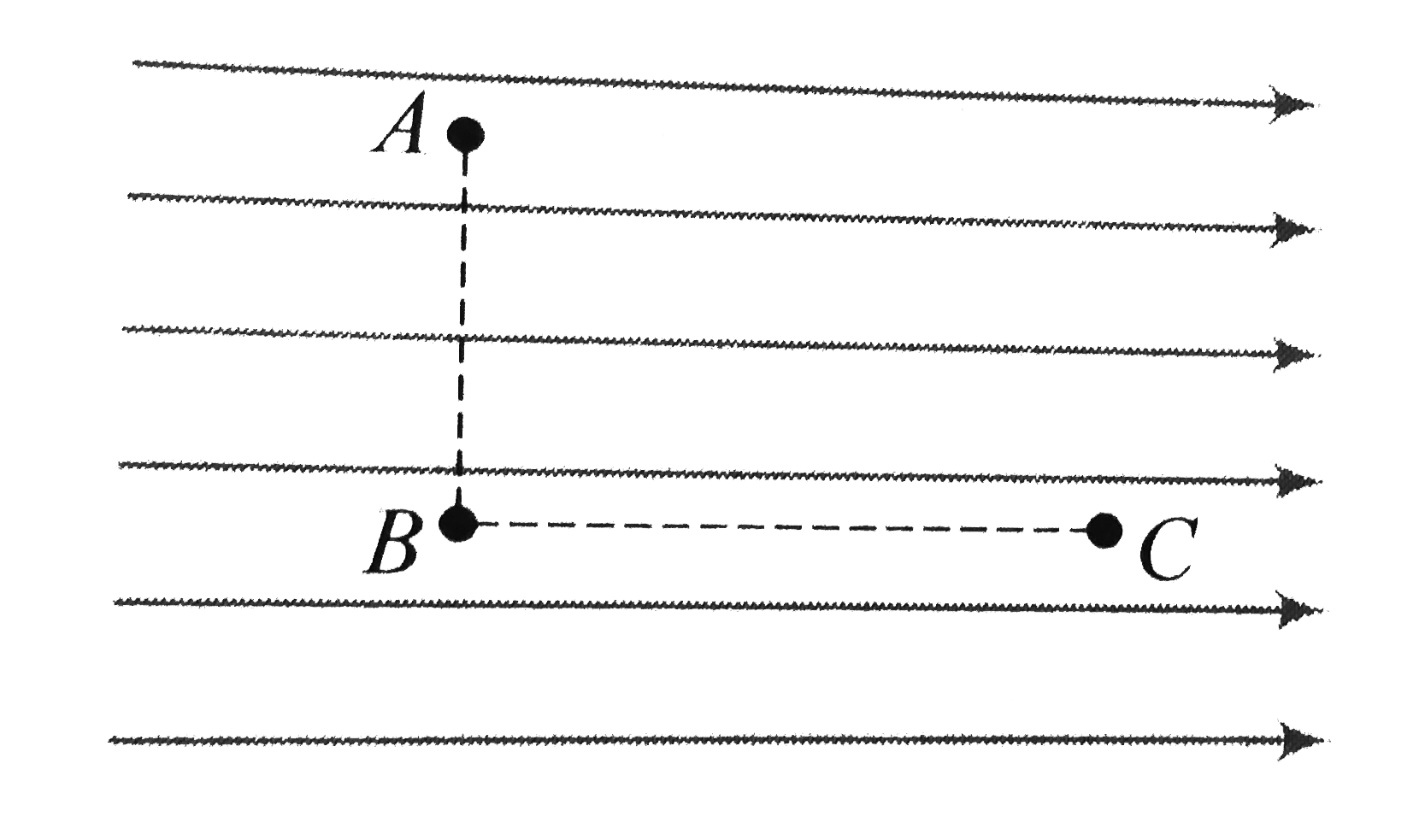 AVA=VB=VCBVA=VB>VCCVA=VB<VCDVA>VB=VC
AVA=VB=VCBVA=VB>VCCVA=VB<VCDVA>VB=VCIf at distance r from a positively charged particle, electric field strength and potential are E and V respectively, which of the following graph (s) is/are correct?
A B
B C
C D
D
A charge +Q at A (see figure) produces electric field E and electric potential V at D. If we now put charges −2Q and +Q at B and C respectively, then the electric field and potential at D will be
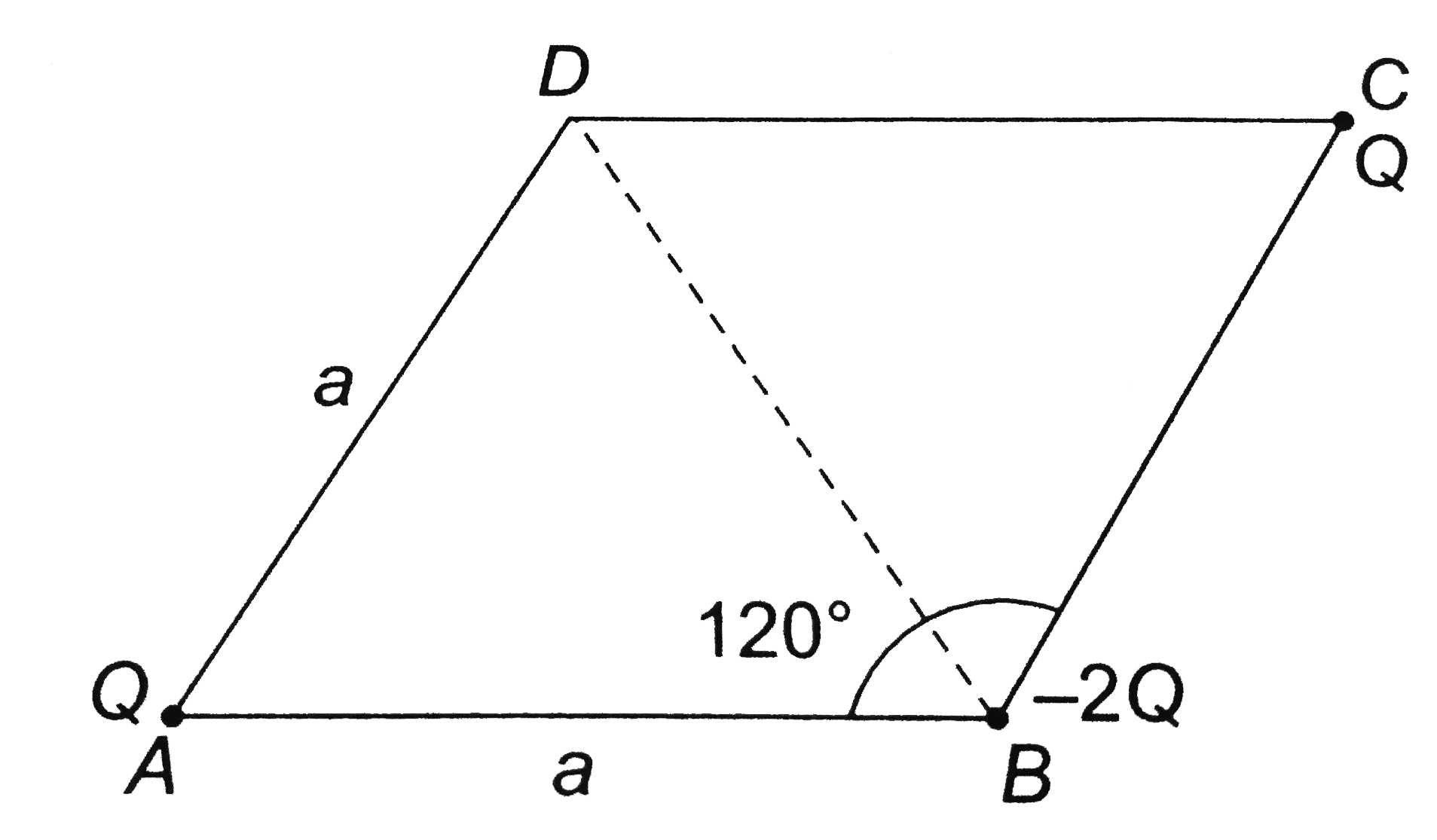 AE and 0B0 and VC√2E and V√2DE√2 and V√2
AE and 0B0 and VC√2E and V√2DE√2 and V√2
Draw a plot showing the variation of (i) electric field E, and (ii) electric potential V with distance 'r' due to a point charge Q.
View SolutionEstablish relation between electric field and potential gradient.
Or
Derive relationship between Electric field intensity and potential gradient at a point in the electric field.
View SolutionAn α particle is placed in an electric field at a point having electric potential 5V. Find its potential energy ?
View SolutionA charge +Q at A (see Fig. 3.140) produces electric field E and electric potential V at D. If we now put charges −3Q and +Q at B and C, respectively, then the electric field and potential at D will be
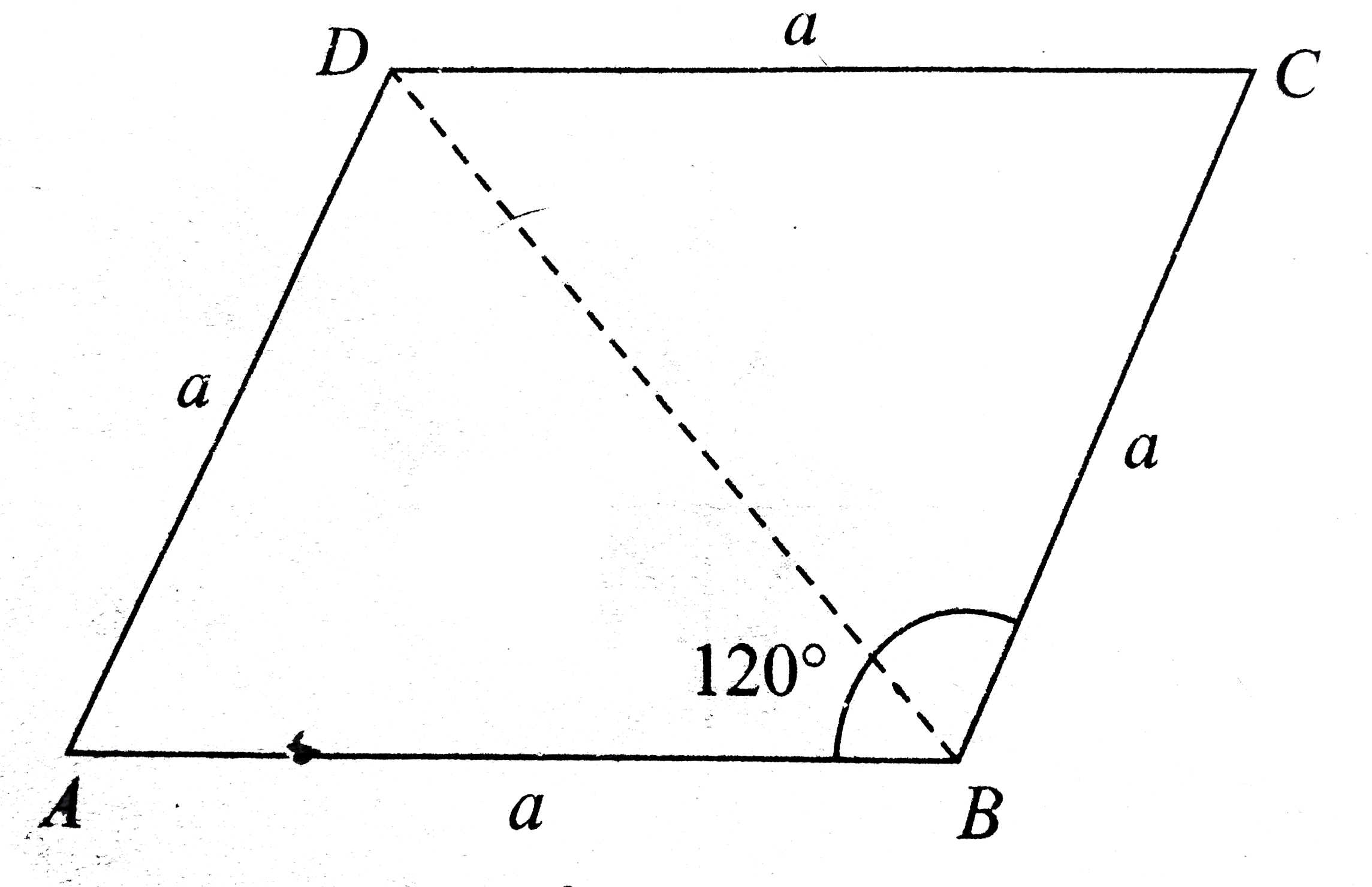 .
.
View SolutionA point dipole is kept at the origin. The potential and electric field due to this dipole on the y-axis at a distance d are, respectively: (Take V = 0 at infinity)
View Solution