A horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
zero
πr2ωB
12Br2ω
Br2ω
The correct Answer is:A
To solve the problem of finding the induced emf in a horizontal ring spinning in a uniform vertical magnetic field, we can follow these steps:
Step 1: Understand the Setup
We have a horizontal ring of radius r that is spinning about its axis with an angular velocity ω. The ring is placed in a uniform vertical magnetic field of magnitude B.
Step 2: Analyze the Magnetic Flux
The magnetic flux Φ through the ring is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the ring,
- θ is the angle between the magnetic field direction and the normal to the surface of the ring.
Since the ring is horizontal and the magnetic field is vertical, the angle θ is 90∘. Thus, cos(90∘)=0.
Step 3: Calculate the Area of the Ring
The area A of the ring can be calculated using the formula for the area of a circle:
A=πr2
Step 4: Determine the Magnetic Flux
Substituting the area into the flux formula:
Φ=B⋅πr2⋅cos(90∘)=B⋅πr2⋅0=0
So, the magnetic flux through the ring is zero.
Step 5: Apply Faraday's Law of Electromagnetic Induction
Faraday's law states that the induced emf E in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦdt
Since the magnetic flux Φ is zero and does not change with time (as both B and A are constant and θ=90∘), we have:
dΦdt=0
Thus, the induced emf is:
E=−0=0
Conclusion
The induced emf in the ring is zero.
We have a horizontal ring of radius r that is spinning about its axis with an angular velocity ω. The ring is placed in a uniform vertical magnetic field of magnitude B.
The magnetic flux Φ through the ring is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the ring,
- θ is the angle between the magnetic field direction and the normal to the surface of the ring.
The area A of the ring can be calculated using the formula for the area of a circle:
A=πr2
Substituting the area into the flux formula:
Φ=B⋅πr2⋅cos(90∘)=B⋅πr2⋅0=0
So, the magnetic flux through the ring is zero.
Faraday's law states that the induced emf E in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦdt
Since the magnetic flux Φ is zero and does not change with time (as both B and A are constant and θ=90∘), we have:
dΦdt=0
Thus, the induced emf is:
E=−0=0
The induced emf in the ring is zero.
Topper's Solved these Questions
Similar Questions
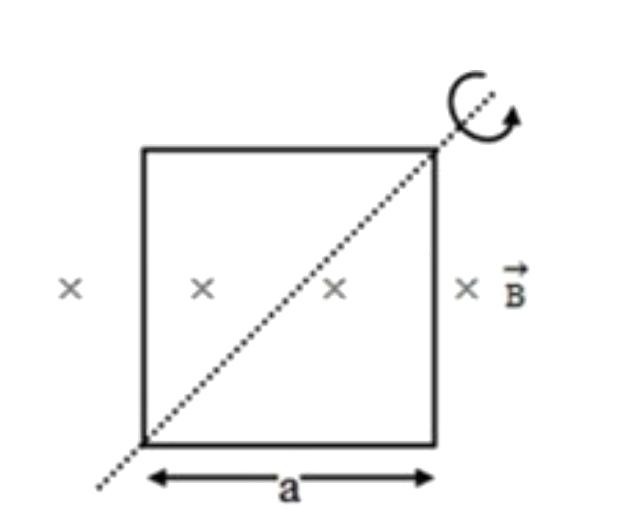
A square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
 View Solution
View SolutionA planar wire loop is placed perpendicular to uniform magnetic field . Wire loop starts rotating in its own plane about its axis with uniform angular velocity ω. If B is magnetic field intensity then what will be the induced emf in the loop ?
View Solution
Knowledge Check
- Question 1 - Select One
A non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23 - Question 2 - Select One
A conductor of length L is rotated about an axis passing through one end of it with an angular velocity ω in a normal and uniform magnetic field B. The emf induced between its end will be -
AωBL2BωBL22CωBL2DωBL - Question 3 - Select One
A metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
 A(a) B2ωr28RB(b) B2ωr22RC( c) B2ωr32RD(d) B2ωr34R
A(a) B2ωr28RB(b) B2ωr22RC( c) B2ωr32RD(d) B2ωr34R
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View SolutionA copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
 View Solution
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
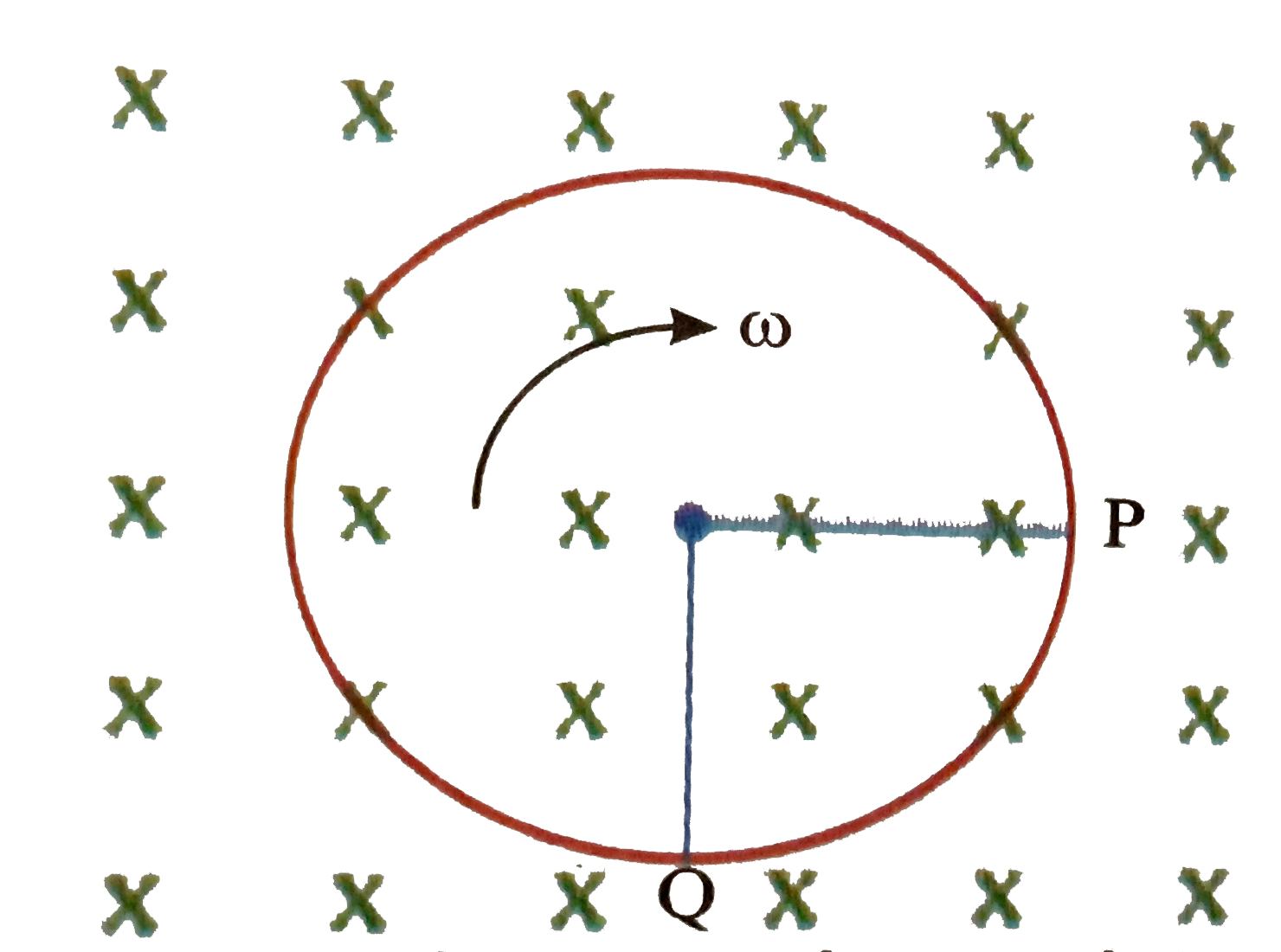
View SolutionA conducting ring of radius 'r' is rolling without slipping with a constant angular velocity ω (figure). If the magnetic field strengh is B and is directed into the page the emf induced across PQ is
 View Solution
View Solution

