A long, straight, hollow conductor (tube) carrying a current has two sections A and C of unequal cross sections joined by a conical section B. 1,2 and 3 are points on a line parallel to the axis of the conductor. The magnetic fields at 1,2 and 3 have magnitudes B1,B2andB3. Then,
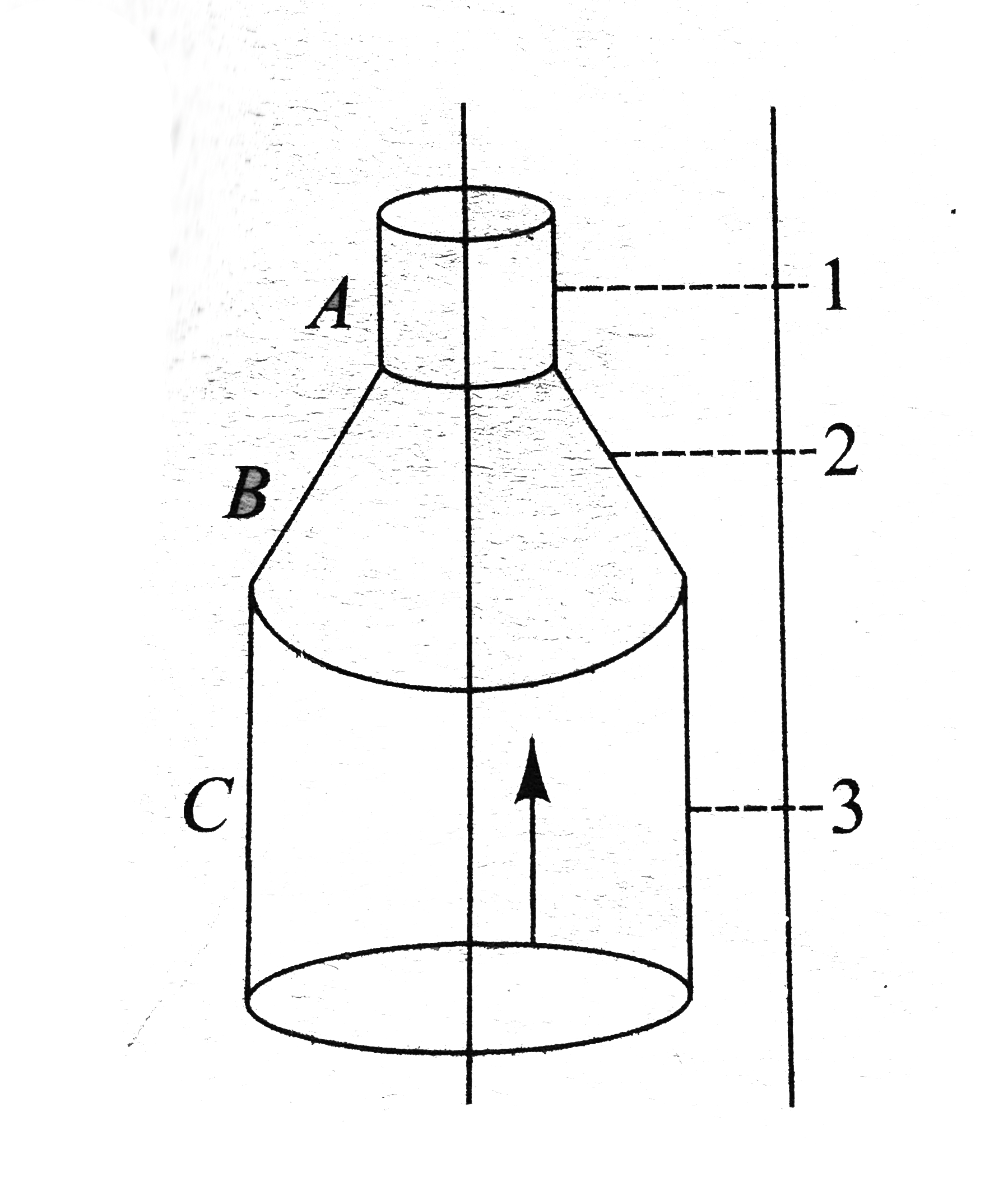
B1=B2=B3
B1=B2≠B3
B1<B2<B3
B2 cannot be found unless the dimensions of the section B are known.
The correct Answer is:A
Step by step video, text & image solution for A long, straight, hollow conductor (tube) carrying a current has two sections A and C of unequal cross sections joined by a conical section B. 1,2 and 3 are points on a line parallel to the axis of the conductor. The magnetic fields at 1,2 and 3 have magnitudes B_1, B_2 and B_3. Then, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A long straight solid conductor of radius 5cm carries a current of 3A, which is uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 4cm from the axis of the conductor. Relative permeability of the conductor=1000.
View SolutionA long straight solid metal rod of radius 4cm carries a current 2A, uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 3cm from the axis of the wire.
View Solution
Knowledge Check
- Question 1 - Select One or More
In the loops shown in fig. all curved section are either semicircles or quarter circles. All the loops carry same current. The magnetic fields at the centre have magnitudes B1,B2,B3andB4. Then,
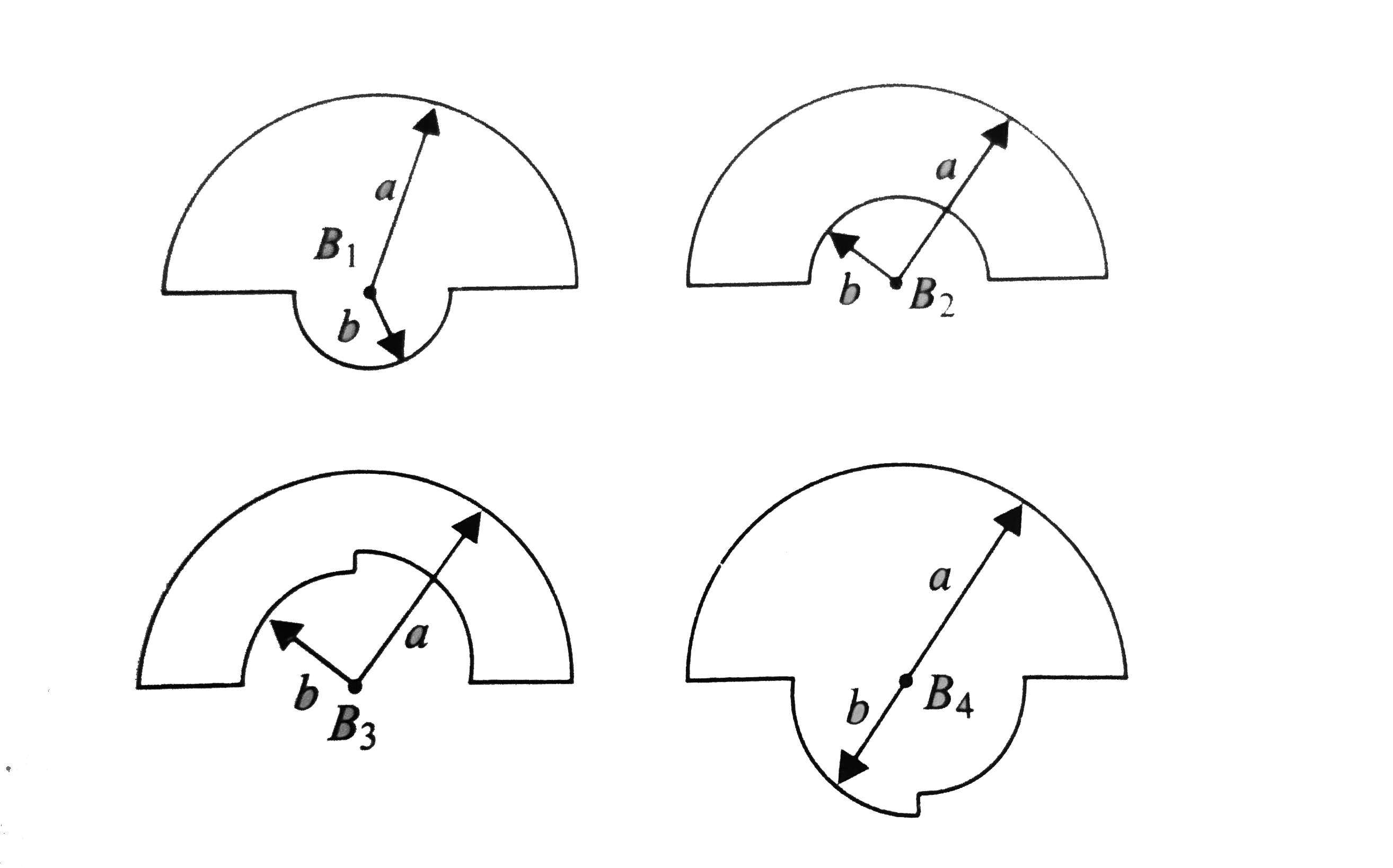 AB4 is maximumBB3 is minimumCB4>B1>B2>B3DB1>B4>B3>B2
AB4 is maximumBB3 is minimumCB4>B1>B2>B3DB1>B4>B3>B2 - Question 2 - Select One
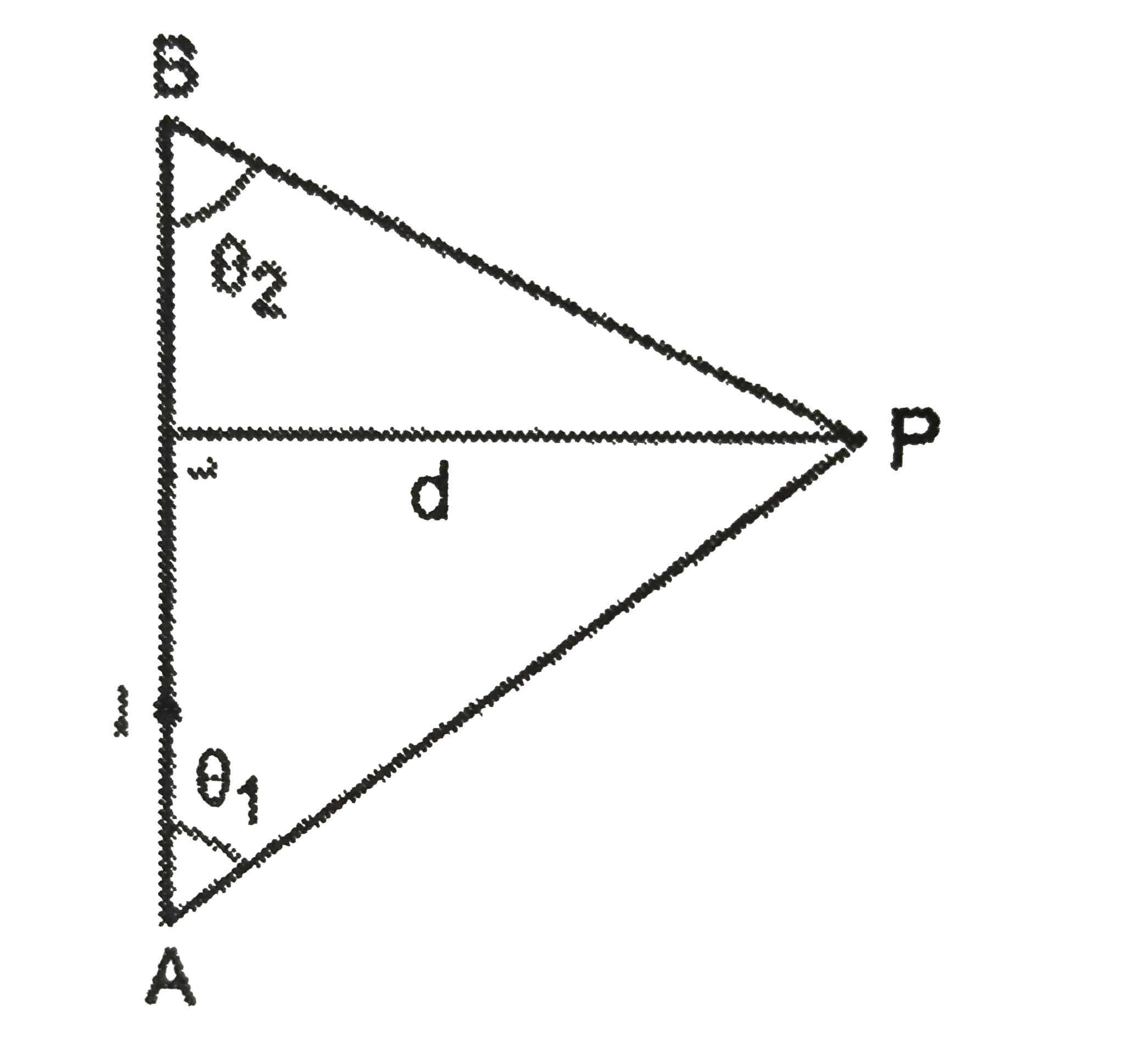
AbB is a section of a straight wire carrying a current I. P is a point at a distance d from AB. The magnetic field at P due to AB has magnitudeAμ0I4πd(cosθ1+cosθ2)Bμ0I4πd(cosθ1−cosθ2)Cμ0I4πd(sinθ1+sinθ2)Dμ0I4πd(sinθ1−sinθ2) - Question 3 - Select One or More
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=r
A long straight solid conductor of radius 5(~cm) carries a current of 2 A waich is uniformly distributed over its circular cross-section. If the magnetic field induction at a distunce of 3 cm from the axis of the conductor is y×10−6T, then find the value of y.
View SolutionA long straight solid conductor of radius 6cm carries a current of 8A, which uniformly distributed over its circular cross-section. Find the magnetic field (a) at a distance of 3cm from the axis of the conductor (b) at a distance 10cm from the axis of the conductor.
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionThe line joining the points (−2,1,−8)and(a,b,c) is parallel to the line whose direction ratios are 6,2,and3. Find the values of a,bandc
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
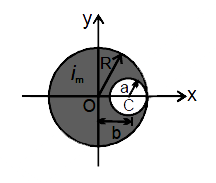
on the y = axis at y = 2R.View Solution

