A very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
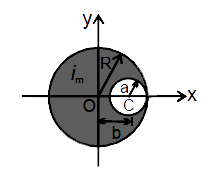
on the y = axis at y = 2R.
Bx=μ0JR(14−a24R2+b2),By=−μ0J2(a2b4R2+b2)
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-I)
33 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-II)
40 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-I)
46 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
A very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
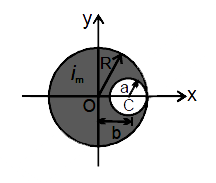
on the x=axis at x = 2R
View SolutionA charge q is uniformly distributed over the surface of a ring-shaped conductor of radius a. Find the field intensity on the axis of the conductor at a distance x from the plane of the conductor.
View Solution
Knowledge Check
Inside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0.
 A0B12μ0→J×→dCμ0→J×→dD32μ0→J×→d
A0B12μ0→J×→dCμ0→J×→dD32μ0→J×→d
A long straight solid conductor of radius 6cm carries a current of 8A, which uniformly distributed over its circular cross-section. Find the magnetic field (a) at a distance of 3cm from the axis of the conductor (b) at a distance 10cm from the axis of the conductor.
View SolutionShow graphically the variation of magnetic field due to a straight conductor of uniform cross-section or radius ‘a’ and carrying steady currently as a function of distance r (a > r) from the axis of the conductor.
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionInside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0.

View SolutionA long straight metal rod has a very long hole of radius a drilled parallel to rod as shown in the figure. If the rod carries a current i. Find the magnetic field (a) on the axis of the rod. (b) on the axis of the hole.

View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View Solution
