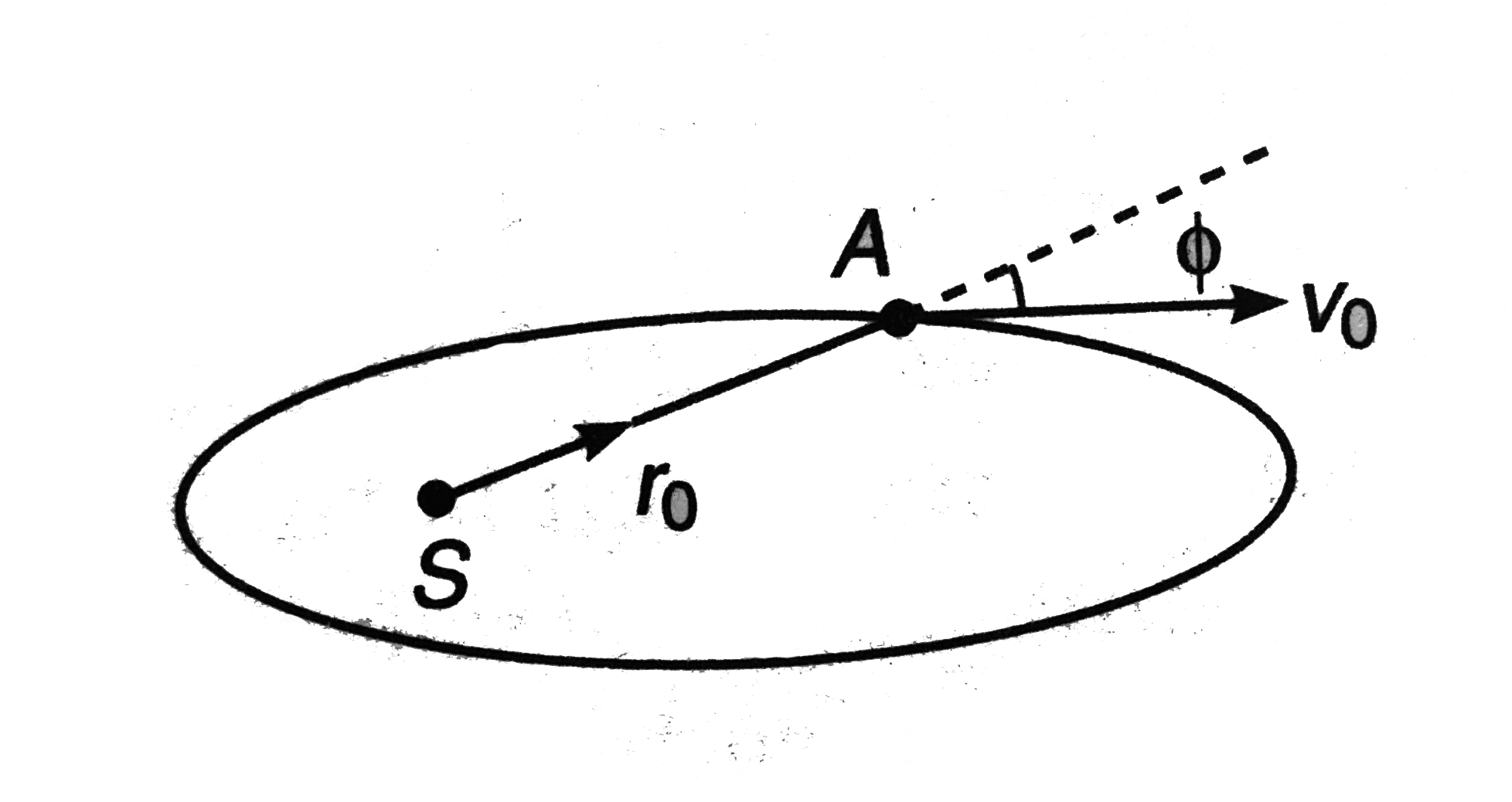
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
The correct Answer is:r02(n−1)[1+√1−4n(n−1)sin2α],r02(n−1)[1−√1−4n(n−1)sin2α)]
Step by step video, text & image solution for A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r_0 from the Sun its velocity was equal to v_0 and the angle between the radius vector r_0 and the velocity vector v_0 was equal to alpha. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Advance MCQs
17 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
Find the maximum and minimum distances of the planet A from the sun S, if at a ceration moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
View SolutionA planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to r1 and r2 respectively. Find the angular momentum M of this planet relative to the centre of the Sun.
View Solution
Knowledge Check
When the Earth in its orbit is at the greatest distance from the Sun, it is at its?
APerigeeBApogeeCPerihelionDApihelionSpeed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
A√GM(2r−1a)B√GM(1r−1a)C√GM(1r−2a)D√GMr2a2A planet moving in a circular orbit around the sun at a distance, 4times theaverage distance of the earth from the sun will complete one revolution in
A8 yearsB4 yearsC16 yearsD1/4 years
A planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionWhat is called the minimum distance from the Sun in a planet in its orbit?
View SolutionWhat is called the maximum distance from the Sun in a planet in its orbit?
View Solution
