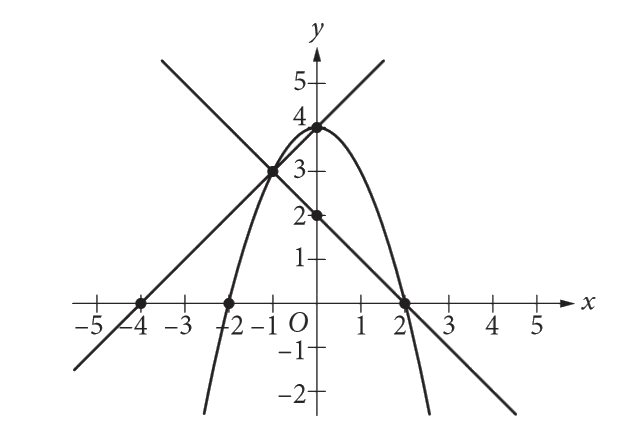
A system of three equations is graphed in the xy-plane above. How many solutions does the system have?
A
None
B
One
C
Two
D
Three
Video Solution
Text Solution
The correct Answer is:B
A solution to the system of three equations is any ordered pair (x, y) that is a solution to each of the three equations. Such an ordered pair (x, y) must lie on the graph of each equation in the xy-plane, in other words, it must be a point where all three graphs intersect. The graphs of all three equations intersect at exactly one point, (−1, 3). Therefore, the system of equations has one solution.
Choice A is incorrect. A system of equations has no solutions when there is no point at which all the graphs intersect. Because the graphs of all three equations intersect at the point (−1, 3), there is a solution. Choice C is incorrect. The graphs of all three equations intersect at only one point, (−1, 3). Since there is no other such point, there cannot be two solutions. Choice D is incorrect and may result from counting the number of points of intersection of the graphs of any two equations, including the point of intersection of all three equations.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One

A system of three equations is shown graphically in the xy-plane above. How many solutions does the system have ?A0B2C3D5 - Question 2 - Select One
(#KPL_SAT_MAT_PRP_PS_10_E01_003_Q01.png" width="80%">
A system of three equation and their graphs are shown above. How many solutions does the system of equations have?ANoneBOneCTwoDThree - Question 3 - Select One
15x + 5y =-8
y+4 =-3x
How many solutions does the system above have ?A0B1C2DAn infinite number
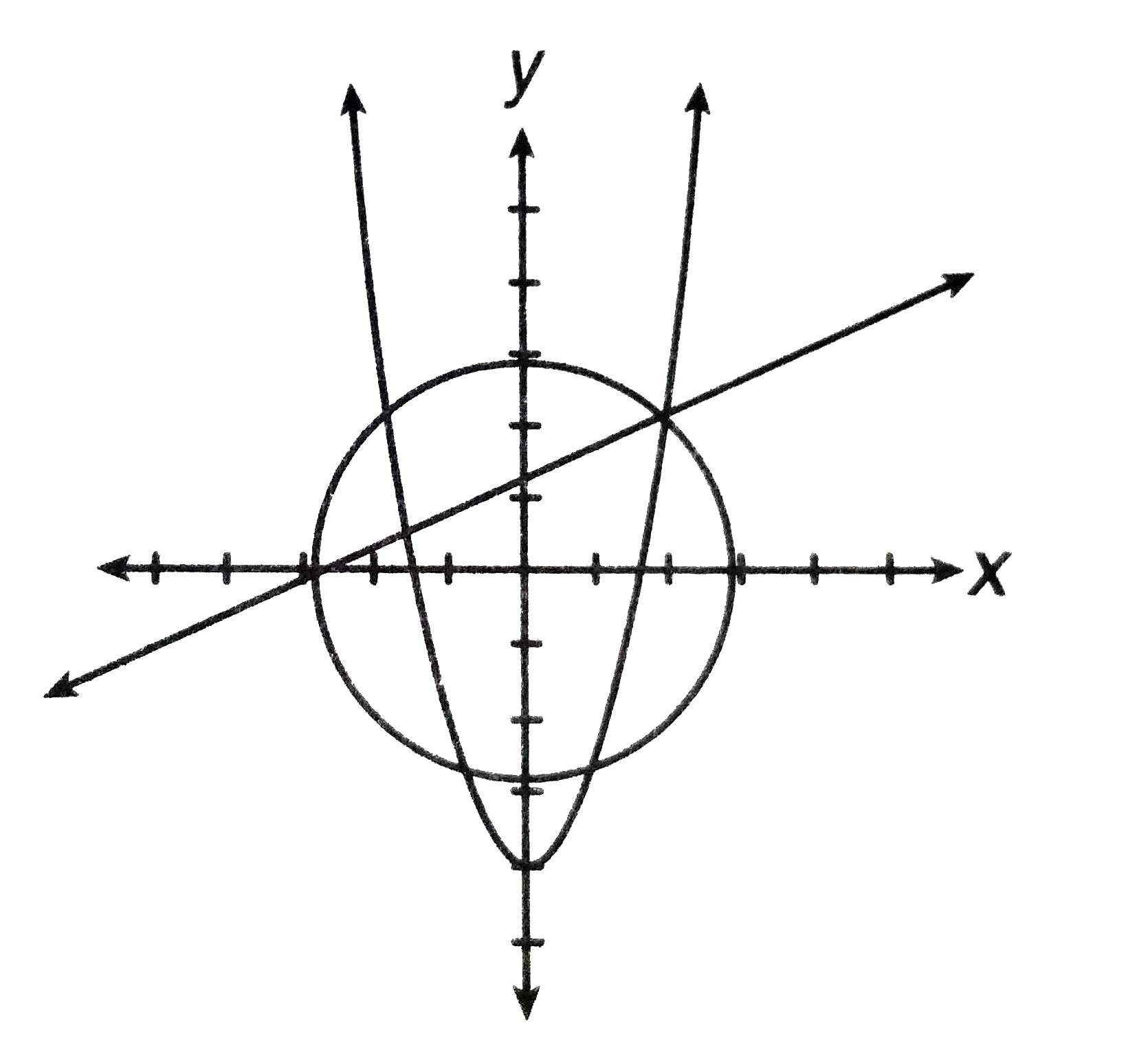
A system of three equations whose graph in the xy-plane are a line, a circle, and a parabola are shown above. How many solutions does the system have?View Solutiony=x2+3
y=15x−33
The system of equations shown above is graphed in the xy-plane. IF system has two solutions, what is the product of the x-coordinates of the two solutions?View Solution
If the system of inequalities y≤2x+1 and y>12x−1 is graphed in the xy-plane above, which quadrant contains no solutions to the system?View Solution2.4x − 1.5y = 0.3
1.6x + 0.5y = −1.3
The system of equations above is graphed in the xy -plane. What is the x -coordinate of the intersection point (x , y) of the system?View Solution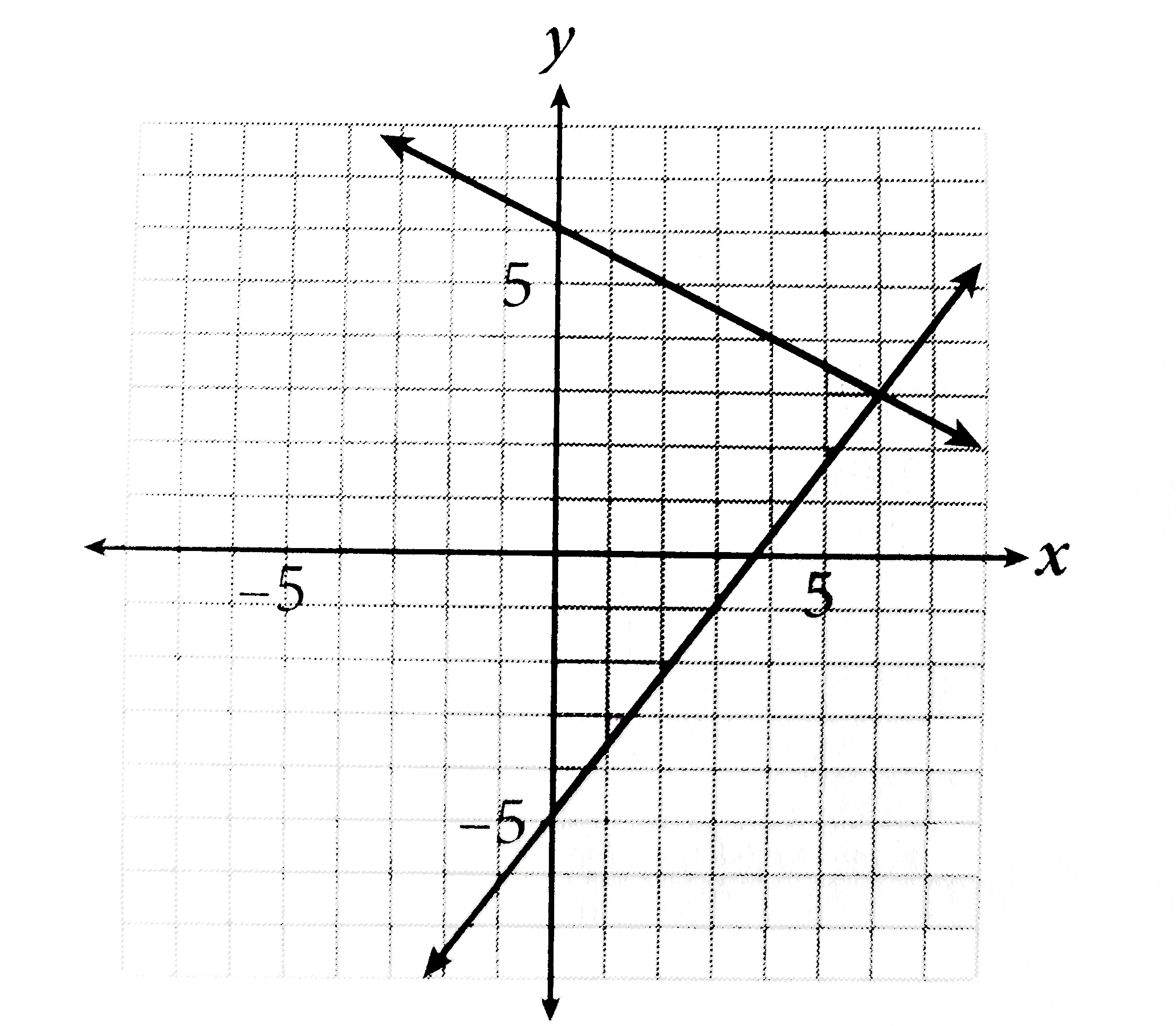
What is tha y-coordinate of the solution to the system shown above ?View Solution


