2.4x − 1.5y = 0.3
1.6x + 0.5y = −1.3
The system of equations above is graphed in the xy -plane. What is the x -coordinate of the intersection point (x , y) of the system?
−0.5
−0.25
0.8
1.75
The correct Answer is:A
The intersection point (x, y) of the two graphs can be found by multiplying the second equation in the system 1.6x + 0.5y = −1.3 by 3, which gives 4.8x + 1.5y = −3.9. The y-terms in the equation 4.8x + 1.5y = −3.9 and the first equation in the system 2.4x − 1.5y = 0.3 have coefficients that are opposites. Adding the left- and right-hand sides of the equations 4.8x + 1.5y = −3.9 and 2.4x − 1.5y = 0.3 produces 7.2x + 0.0y = −3.6, which is equivalent to 7.2x = −3.6. Dividing both sides of the equation by 7.2 gives x = −0.5. Therefore, the xcoordinate of the intersection point (x, y) of the system is −0.5.
Choice B is incorrect. An x-value of −0.25 produces y-values of −0.6 and −1.8 for each equation in the system, respectively. Since the same ordered pair doesn’t satisfy both equations, neither point can be the intersection point. Choice C is incorrect. An x-value of 0.8 produces y-values of 1.08 and −5.16 for each equation in the system, respectively. Since the same ordered pair doesn’t satisfy both equations, neither point can be the intersection point. Choice D is incorrect. An x-value of 1.75 produces y-values of 2.6 and −8.2 for each equation in the system, respectively. Since the same ordered pair doesn’t satisfy both equations, neither point can be the intersection point.
Similar Questions

The tables above represent data points for two linear equations. If the two equations form a system, what is the x-coordinate of the solution to that system ?05:01View SolutionIf (x,y) is a solution to the system of equations above, what is the value of x2 ?
01:17View SolutionIn the xy-plane, which of the following is a point of intersection between the graphs of y=x+2andy=x2+x−2?
04:15View Solution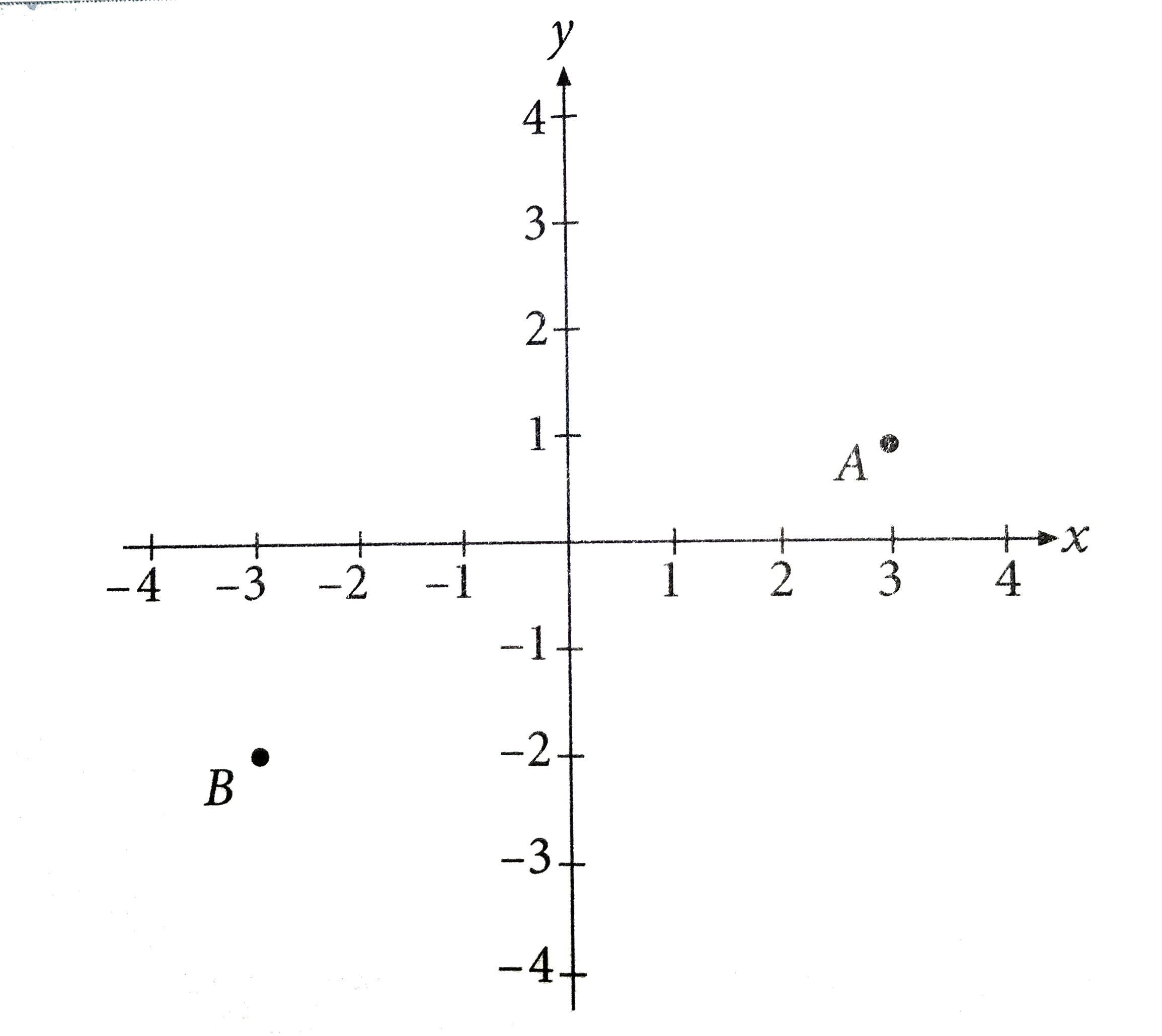
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?02:25View Solutiony=x2−4,x+y=2
Based on the system of equations above , what is the minimum value of the product xy ?02:09View Solution
The lines graphed in the xy-plane above represent a system of two linear equations. What is the solution (x,y) to the system?View Solutiony=x2+3
y=15x−33
The system of equations shown above is graphed in the xy-plane. IF system has two solutions, what is the product of the x-coordinates of the two solutions?03:33View SolutionThe value of x and y in the equation 0.2x+0.3y=1.3 and 0.4x+0.5y=2.3 are :
View Solution

