y=−(x−3)2+a
In the equation above, a is a constant. The graph of the equation in the xy-plane is a parabola. Which of the following is true about the parabola?
Its minimum occurs at (−3, a).
Its minimum occurs at (3, a).
Its maximum occurs at (−3, a).
Its maximum occurs at (3, a).
The correct Answer is:D
The vertex form of a quadratic equation isy=n(x−h)2+k, where (h, k) gives the coordinates of the vertex of the parabola in the xy-plane and the sign of the constant n determines whether the parabola opens upward or downward. If n is negative, the parabola opens downward and the vertex is the maximum. The given equation has the values h = 3, k = a, and n = −1. Therefore, the vertex of the parabola is (3, a) and the parabola opens downward. Thus, the parabola’s maximum occurs at (3, a)
Choice A is incorrect and may result from interpreting the given equation as representing a parabola in which the vertex is a minimum, not a maximum, and from misidentifying the value of h in the given equation as −3, not 3. Choice B is incorrect and may result from interpreting the given equation as representing a parabola in which the vertex is a minimum, not a maximum. Choice C is incorrect and may result from misidentifying the value of h in the given equation as not 3.
Similar Questions
In the xy-plane , a line that has the equation y=c for some constant c intersects a parabola at exactly one point. If the parabola has the equation y=−x2+5x, what is the value of c ?
03:23View Solution
The vertex of the parabola in the xy plane above is (0, c). Which of the following is true about the parabola with the equation y=−a(x−b)2+c ?01:15View SolutionIn the xy-plane, the parabola with equation y=(x−11)2 intersects the line with equation y = 25 at two points, A and B. What is the length of ¯¯¯¯¯¯AB ?
05:32View Solutiony=a(x−2)(x+4)
In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c,d) . Which of the following is equal to d ?02:29View Solutiony=x2−6x+8
The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the x-intercepts of the parabola as constants or coefficients?01:50View Solutiony=x2−a
In the equation above a is a positive constant and the graph of the equation in the xy-plane is a parabola. Which of the following is an equivalent form of the equation?01:29View Solution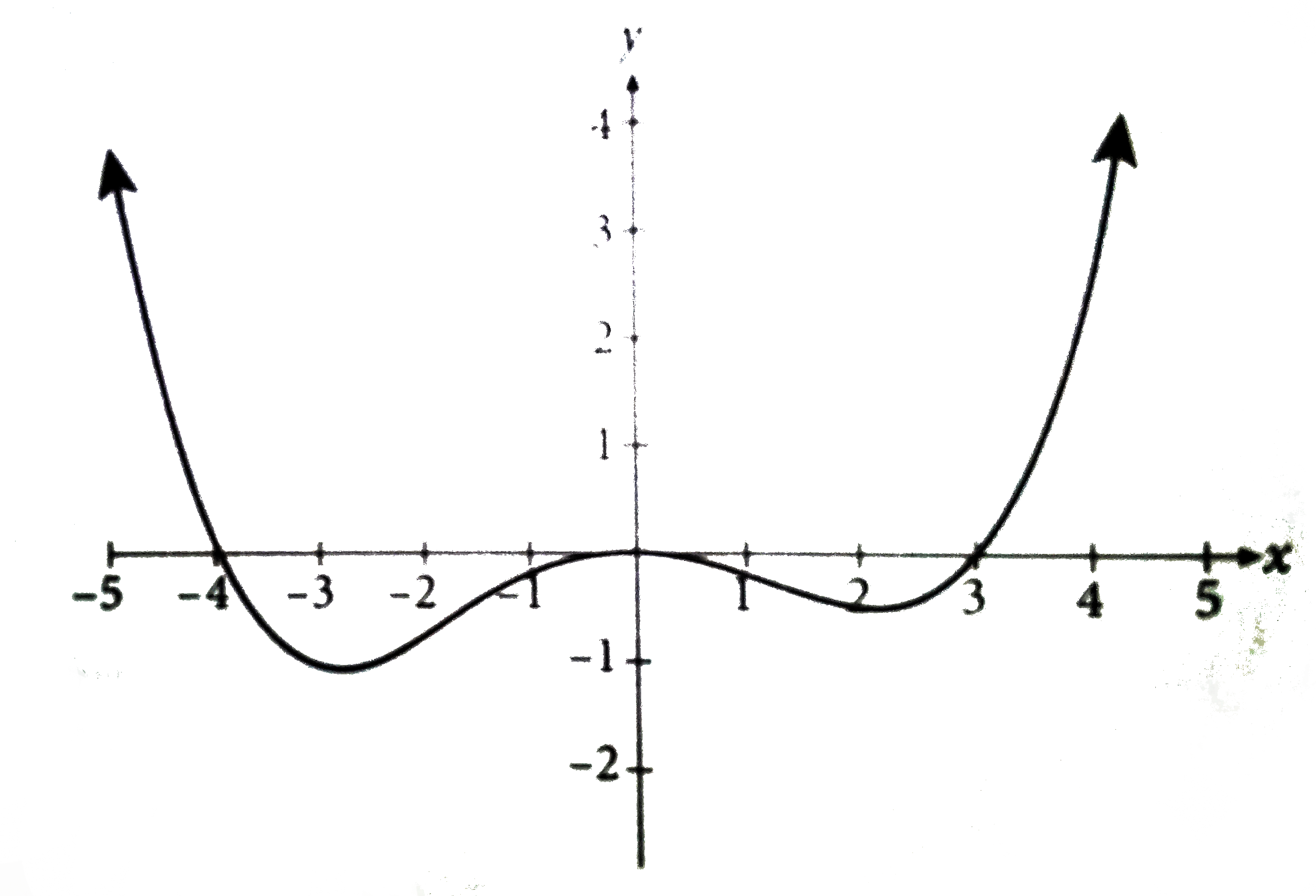
Which of the following could be the equation of the graph in the xy-plane shown above?02:43View Solution

