In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c,d) . Which of the following is equal to d ?
The correct Answer is:A
To find the value of d in the quadratic equation y=a(x−2)(x+4), we will follow these steps:
Step 1: Identify the Roots
The roots of the quadratic equation can be found by setting y=0:
a(x−2)(x+4)=0
This gives us the roots:
1. x−2=0 → x=2
2. x+4=0 → x=−4
Step 2: Find the x-coordinate of the Vertex
The x-coordinate of the vertex of a parabola can be found by taking the average of the roots:
xvertex=x1+x22=2+(−4)2=−22=−1
Step 3: Substitute x-coordinate into the Equation
Now that we have the x-coordinate of the vertex, we can substitute x=−1 back into the original equation to find d:
y=a(−1−2)(−1+4)
Calculating the values inside the parentheses:
y=a(−3)(3)
Thus,
y=−9a
Step 4: Conclusion
The y-coordinate of the vertex, d, is equal to:
d=−9a
The roots of the quadratic equation can be found by setting y=0:
a(x−2)(x+4)=0
This gives us the roots:
1. x−2=0 → x=2
2. x+4=0 → x=−4
The x-coordinate of the vertex of a parabola can be found by taking the average of the roots:
xvertex=x1+x22=2+(−4)2=−22=−1
Now that we have the x-coordinate of the vertex, we can substitute x=−1 back into the original equation to find d:
y=a(−1−2)(−1+4)
Calculating the values inside the parentheses:
y=a(−3)(3)
Thus,
y=−9a
The y-coordinate of the vertex, d, is equal to:
d=−9a
Similar Questions
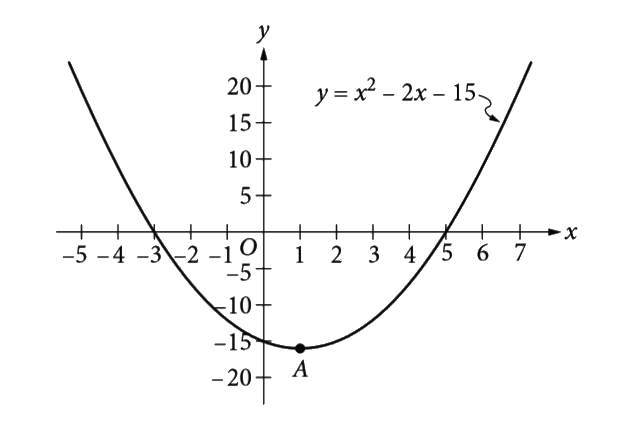
Which of the following is an equivalent form of the equation of the graph shown in the xy-plane above, from which the coordinates of vertex A can be identified as constants in the equation?01:59View Solutiony=x2−6x+8
The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the x-intercepts of the parabola as constants or coefficients?01:50View Solutionf(x)=2x+1
The function f is defined by the equation above which of the following is the graph of y=−f(x) in the xy-plane?02:35View Solutiony=x2−a
In the equation above a is a positive constant and the graph of the equation in the xy-plane is a parabola. Which of the following is an equivalent form of the equation?01:29View Solution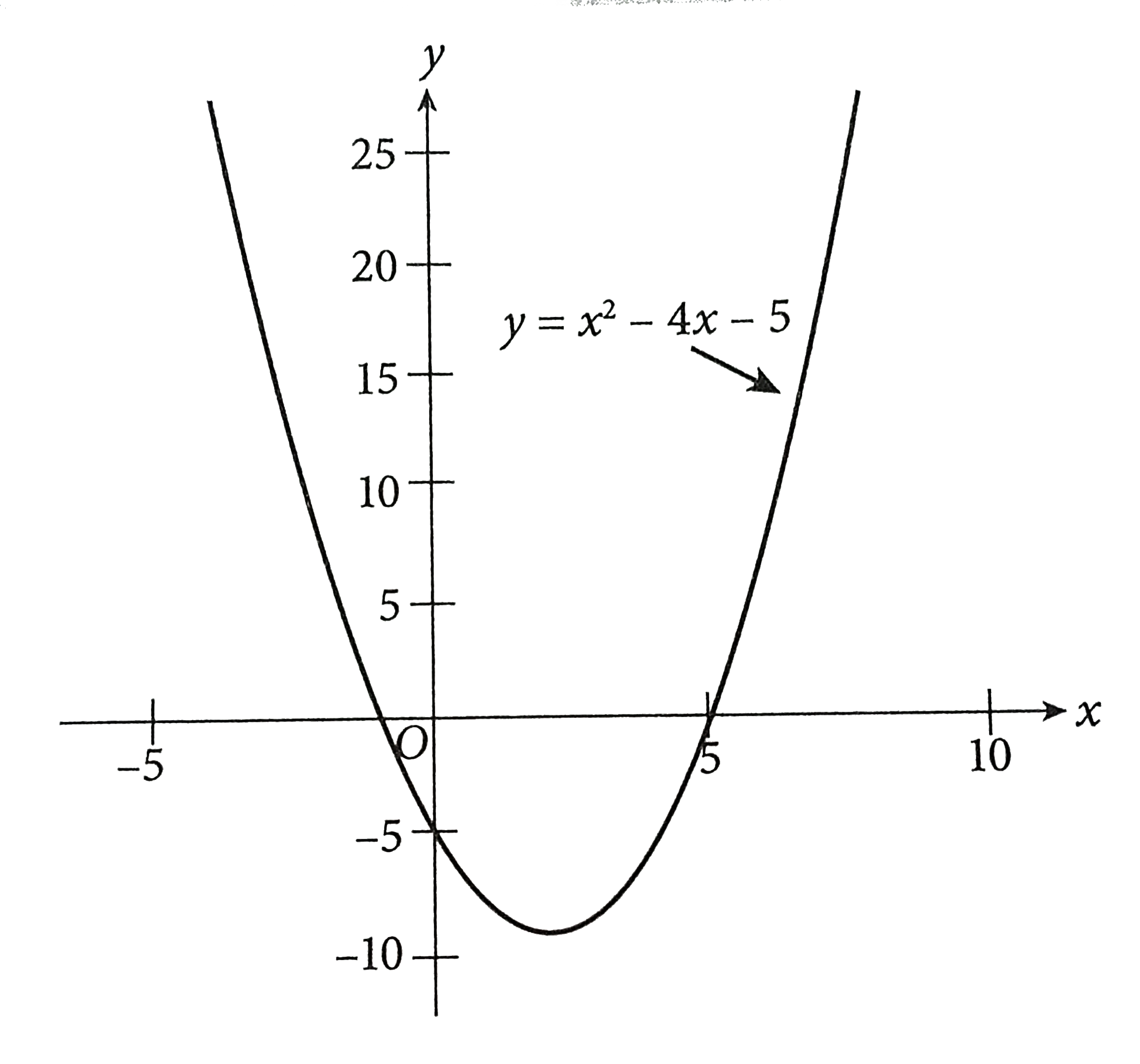
Which of the following is an equivalent form of the equation of the graph shown in the xy plane above, from which the coordinates of vertex Z can be identified as constant in the equation?02:19View Solution
Which of the following is an equivalent form of the equation of the graph shown in the xy-plane above, from which the coordinates of vertex V can be identified from constants in the equation?03:41View Solutiony=x2+16x+28
The equation above represents the graph of a parabola in the xy-plane. Which of the following represents an equivalent form of the equation that includes the minimum value of y as a constant?03:03View Solution

