Three point masses m1=2Kg,m2=4kgandm3=6kg are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
To find the center of mass of the three point masses located at the corners of an equilateral triangle, we will follow these steps:
Step 1: Define the positions of the masses
Let’s place the equilateral triangle in the coordinate system:
- Mass m1=2kg at point A(0,0)
- Mass m2=4kg at point B(1,0)
- Mass m3=6kg at point C(12,√32)
Step 2: Calculate the total mass
The total mass M is given by:
M=m1+m2+m3=2kg+4kg+6kg=12kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is calculated using the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(2⋅0)+(4⋅1)+(6⋅12)12
xcm=0+4+312=712
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is calculated using the formula:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(2⋅0)+(4⋅0)+(6⋅√32)12
ycm=0+0+3√312=√34
Step 5: Write the final coordinates of the center of mass
Thus, the coordinates of the center of mass Rcm are:
Rcm=(712,√34)
Final Answer
The location of the center of mass of the three point masses is (712,√34).
---
Let’s place the equilateral triangle in the coordinate system:
- Mass m1=2kg at point A(0,0)
- Mass m2=4kg at point B(1,0)
- Mass m3=6kg at point C(12,√32)
The total mass M is given by:
M=m1+m2+m3=2kg+4kg+6kg=12kg
The x-coordinate of the center of mass xcm is calculated using the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(2⋅0)+(4⋅1)+(6⋅12)12
xcm=0+4+312=712
The y-coordinate of the center of mass ycm is calculated using the formula:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(2⋅0)+(4⋅0)+(6⋅√32)12
ycm=0+0+3√312=√34
Thus, the coordinates of the center of mass Rcm are:
Rcm=(712,√34)
The location of the center of mass of the three point masses is (712,√34).
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Check points50videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
If three point masses m1,m2andm3 are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View Solution
Knowledge Check
- Question 1 - Select One
Three particles of masses m1=1kg,m2=2kg and m3=3kg are kept at the vertices of an equilateral triangle of side 1 m. What is the x co-ordinate of its centre of mass?
A34mB45mC67mD712m - Question 2 - Select One
Three point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
A(m1+m2)a24B(m2+m3)a24C(m1+m3)a24D(m1+m2+m3)a24 - Question 3 - Select One
The centre of masses of three particles of mass m1=m2=m3=1 kg at the corners of an equilateral triangle of side 1 m will be -
A0.50m, 0.29mB0.43m, 0.50mC0.25m, 0.25mD0.22m, 0.22m
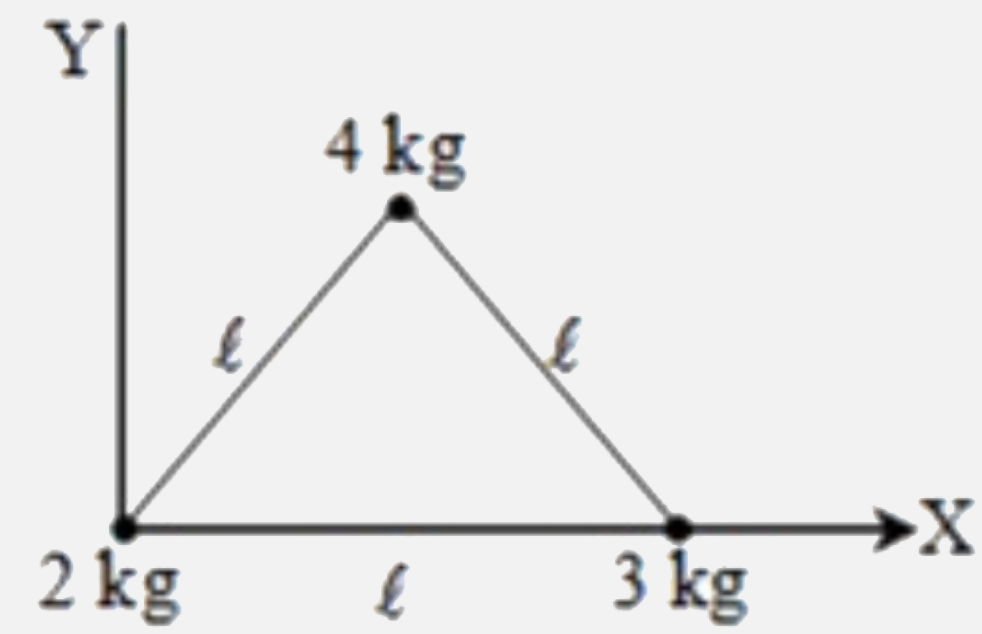
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
 View Solution
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionThree spherical balls of masses 1 kg, 2 kg and 3 kg are placed at the corners of an equilaterial triangle of side 1m.Find the magnitude of the gravitational force exerted by 2 kg and 3 kg masses on 1 kg mass.
View SolutionThree sperical balls of masses 1kg,2kg and 3kg are placed at the corners of an equilateral triangle of side 1m. Find the magnitude of the gravitational force exerted by 2kg and 3kg masses on 1kg mass.
View Solution

