A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

According to the question,
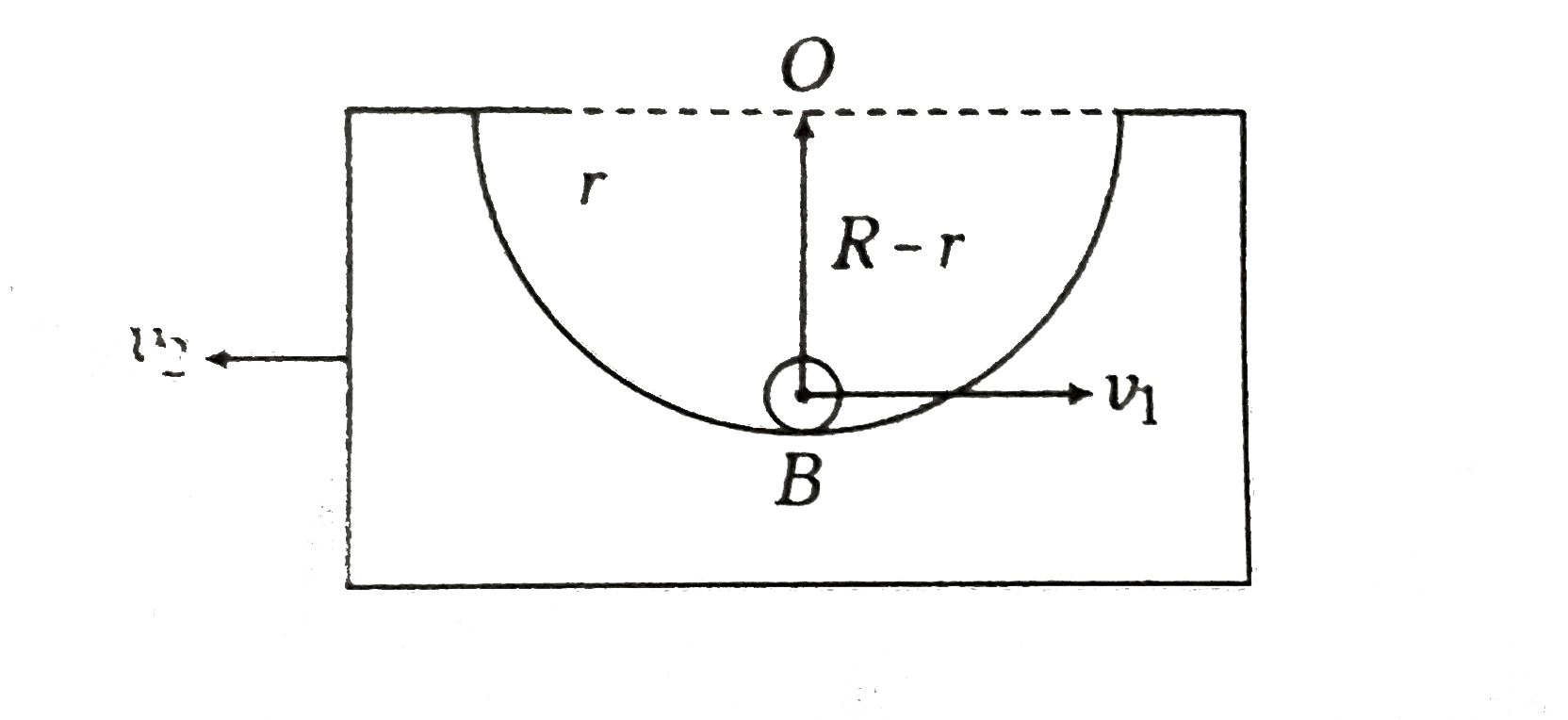
When the sphere reaches at B
Let v1 = velocity of m
v2 = velocity of M
By the momentum conseration in the horizontal direction.
m1v1=Mv22
Applying the energy conservation between A and B
mg(R−r)=12mv21+Mv22
Solving, v1=(sqrt(2Mg(R-r))/(M+m)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Check points50videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
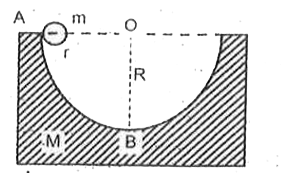
A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
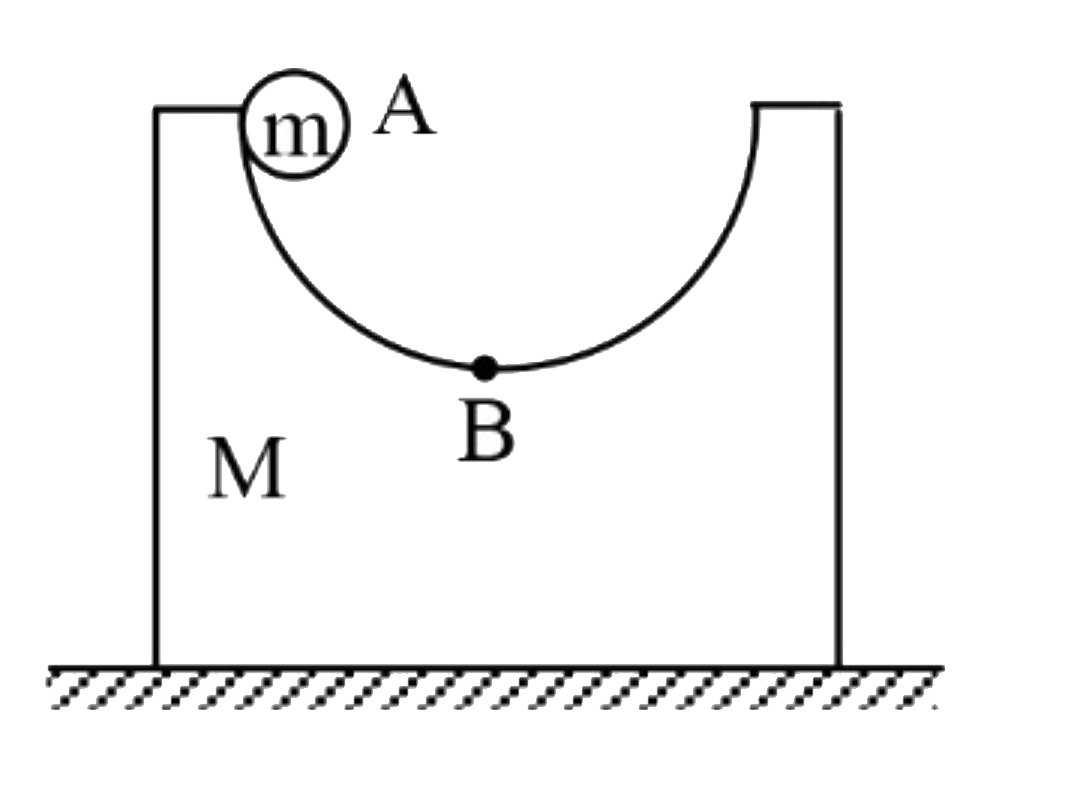 A√103ms−1B√43ms−1C√52ms−1D√10ms−1
A√103ms−1B√43ms−1C√52ms−1D√10ms−1 - Question 2 - Select One
A circular rope of weight W and radius r=R2 is resting on a smooth sphere of radius R The tension in rope is
 AW/(π√6)BW/(π√12)CW/(π√10)Dnone of these
AW/(π√6)BW/(π√12)CW/(π√10)Dnone of these - Question 3 - Select One
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
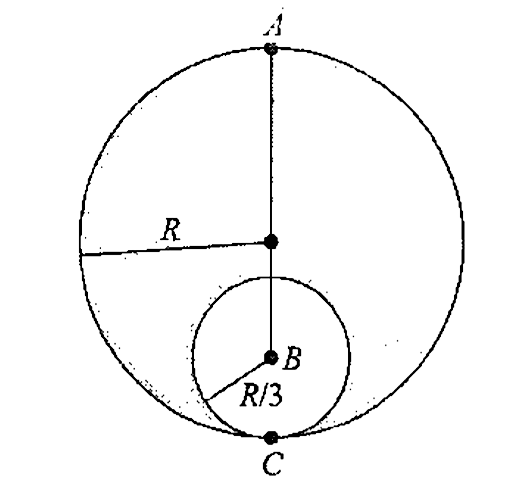 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
 View Solution
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
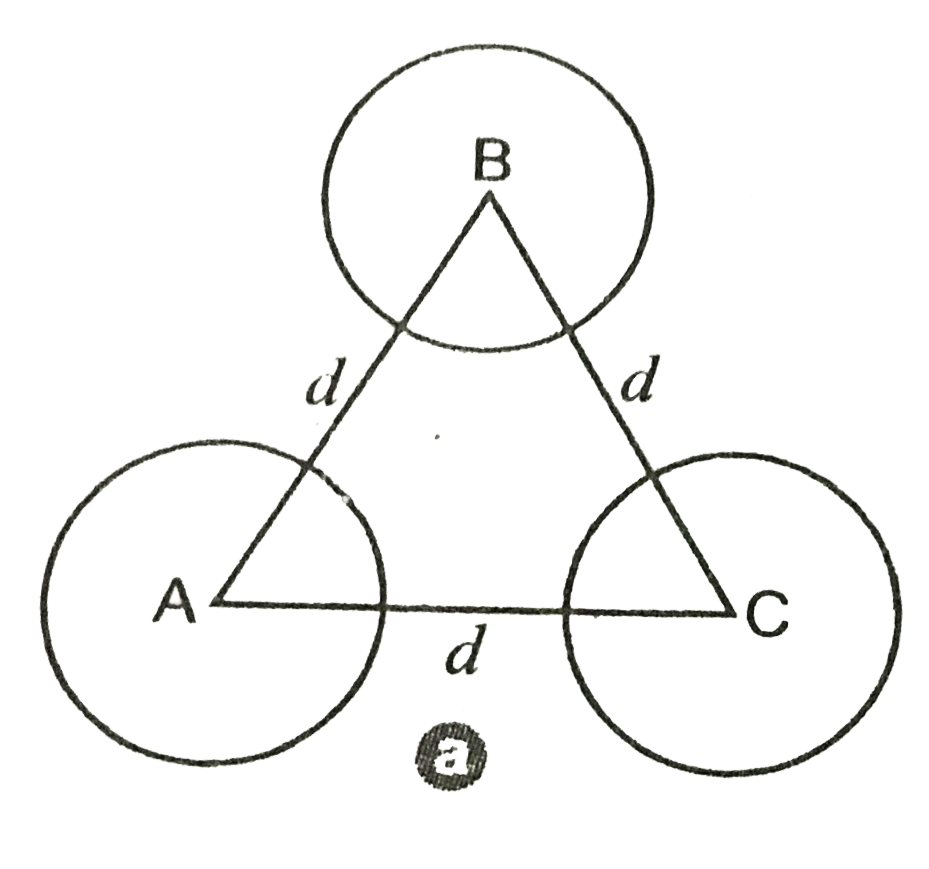 View Solution
View SolutionA block of mass m is suspended from a pulley in form of a circular disc of mass m & radius R. The system is released from rest, find the angular velocity of disc when block has dropped by height h. (there is no slipping between string & pulley)
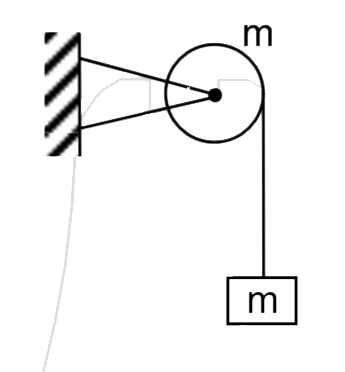 View Solution
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
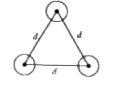 View Solution
View SolutionIn the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
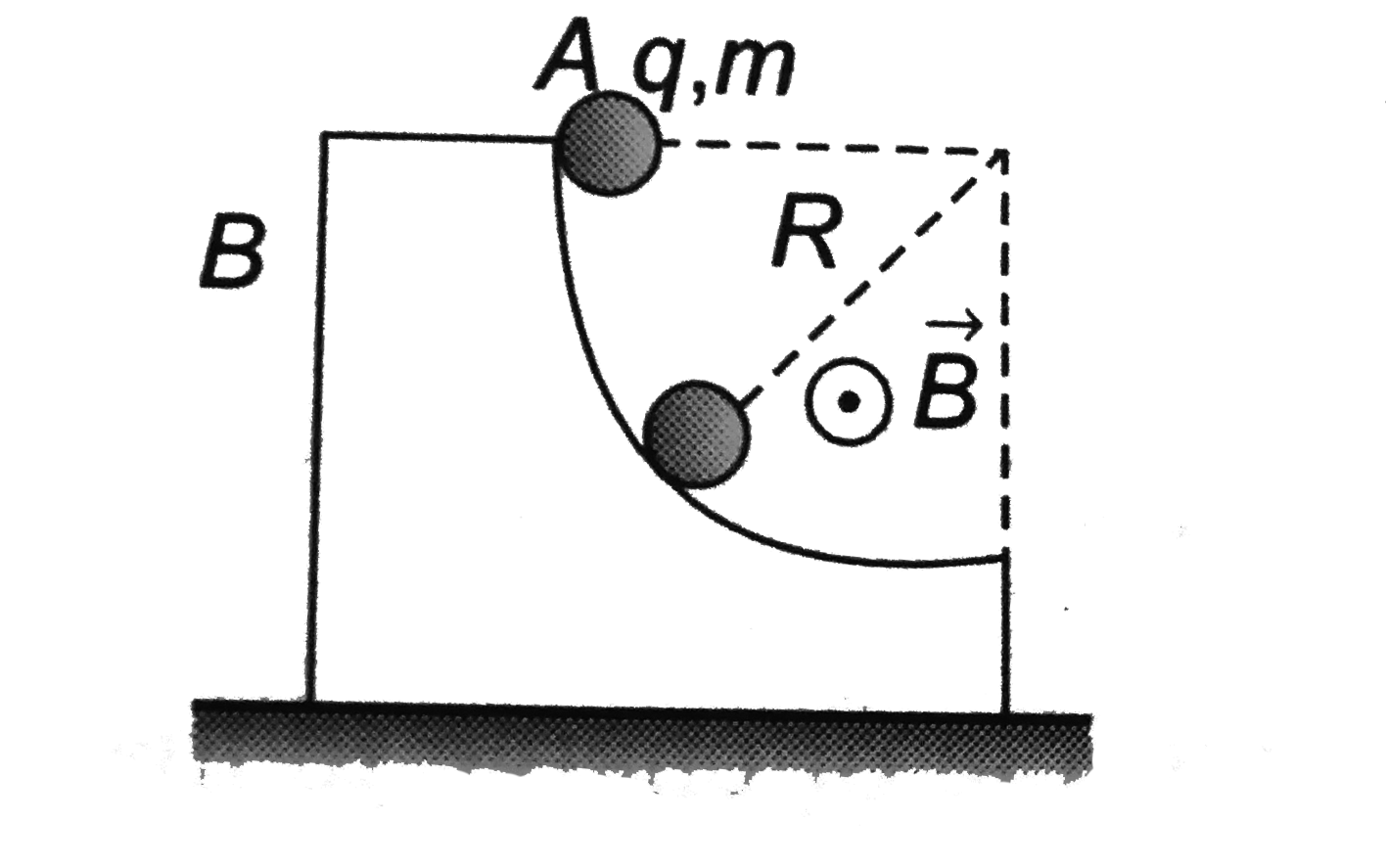 View Solution
View Solution

