A rod has length 'l' and mass per unit length linearly increases from λ to 2λ as shown in figure. Rod rotates with constant angular velocity ω in a gravity free space. Find the tension (in Newton) in the rod at its middle point. (take ωl=2m/secandλ=3kg/m)

The correct Answer is:8
Step by step video, text & image solution for A rod has length 'l' and mass per unit length linearly increases from lamda to 2 lamda as shown in figure. Rod rotates with constant angular velocity omega in a gravity free space. Find the tension (in Newton) in the rod at its middle point. (take omegal=2m//sec and lamda = 3 kg//m) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point45videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together67videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Matrix Matching7videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA thin rod of mass m and length l is rotated in a horizontal plane about one of its ends with a constant angular speed ω in gravity free space.Then the tension at the midpoint of the rod is 3mlω2p.The value of p is?
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then :
ATension in ring is zeroBTension will vary at all pointsCTension is constant throughout ringDTension in string is mω2r2 - Question 2 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 3 - Select One or More
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)
As shown in the figure, a rod moves with v = 2 m/sec & rotates with ω=2π rad/sec. Find the point on the rod whose velocity is zero in this frame.
 View Solution
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
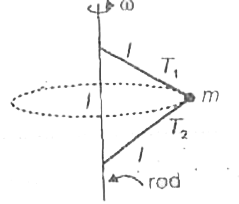 View Solution
View SolutionA midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.
 View Solution
View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.
 View Solution
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
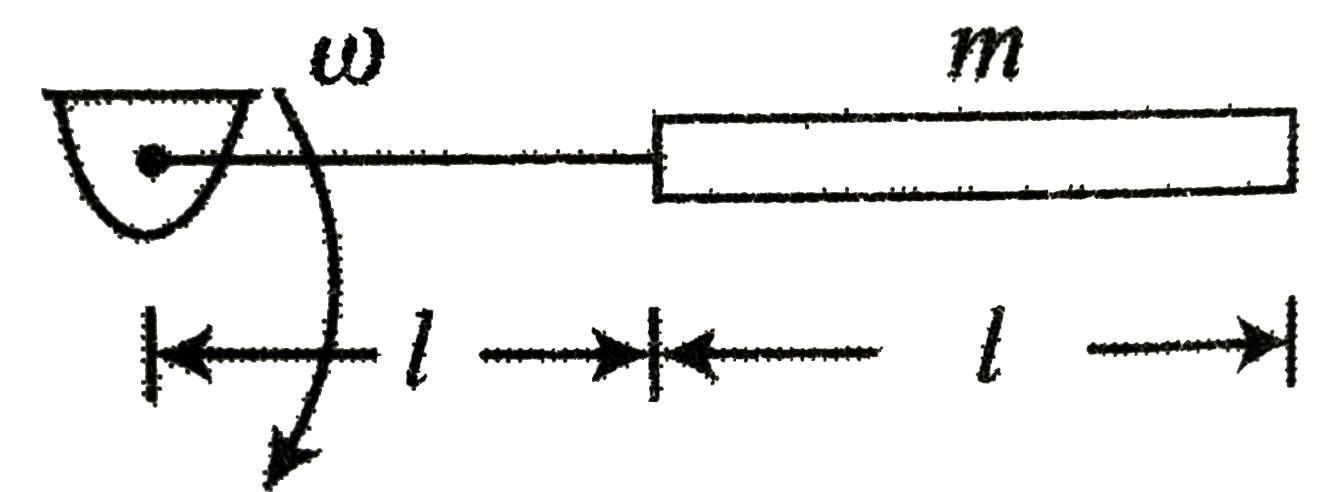
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.View Solution

