A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of P to the kinetic energy of S is:
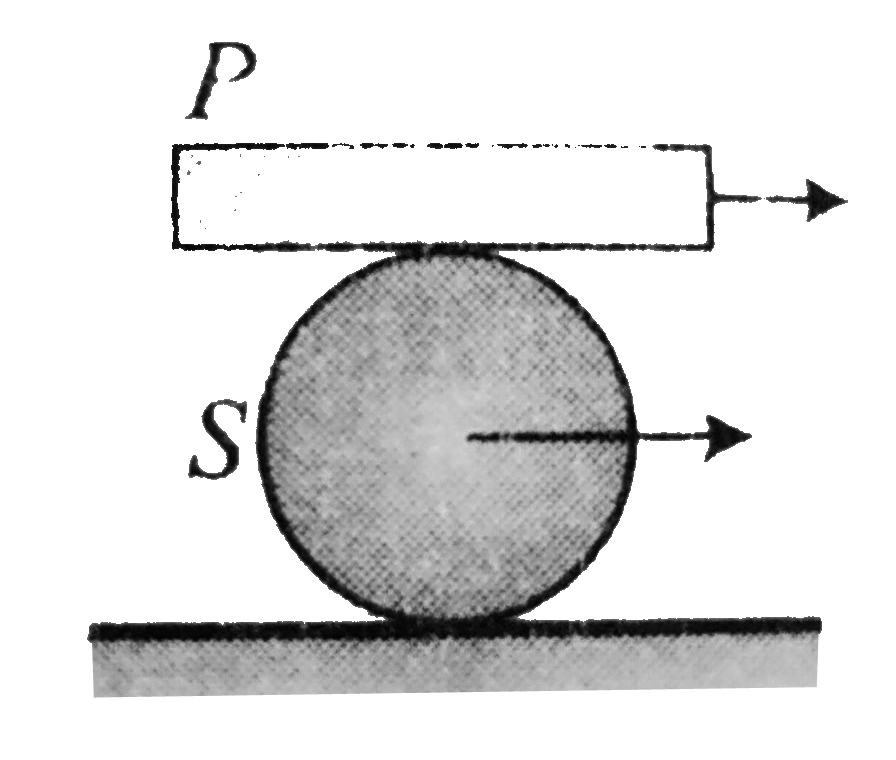
1:1
2:1
8:3
5:3
The correct Answer is:C
Step by step video, text & image solution for A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of P to the kinetic energy of S is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
Knowledge Check
- Question 1 - Select One
A hollow sphere rolls without slipping on plane surface. The ratio of kinetic energy of rotation to the total kinetic energy is
A1/3B2/5C1/4D3/4 - Question 2 - Select One
In the figure shown mass of both, the spherical body and block is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
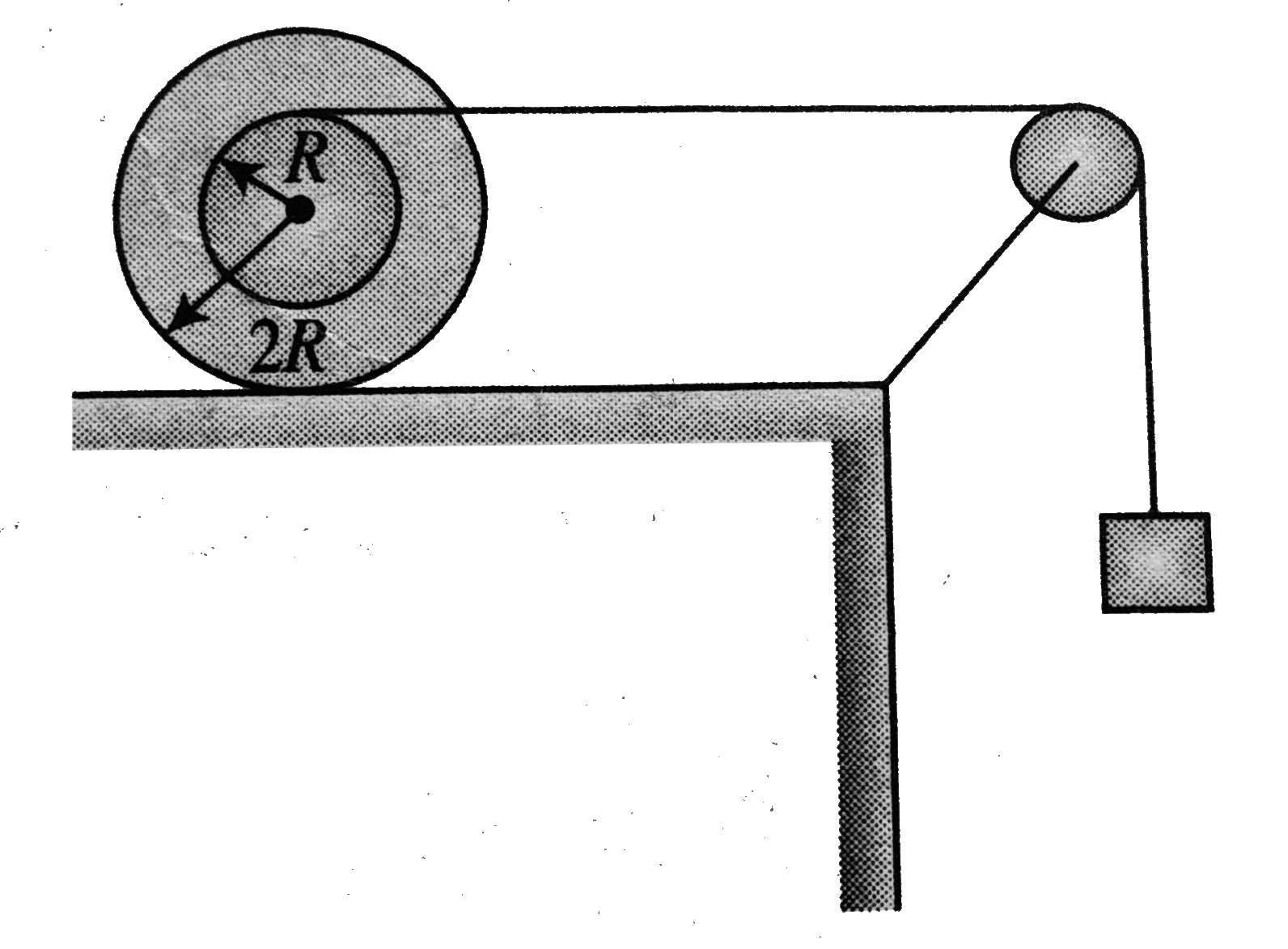 A3/4B1/3C2/3D1/2
A3/4B1/3C2/3D1/2 - Question 3 - Select One
A sphere is rolling down an inclined plane without slipping. The ratio of rotational kinetic energy to total kinetic energy is
A57B254C27Dnone of the above
A ring is rolling without slipping. The ratio of translational kinetic energy to rotational kinetic energy is
View SolutionA solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionIn the figure shon mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no sliiping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
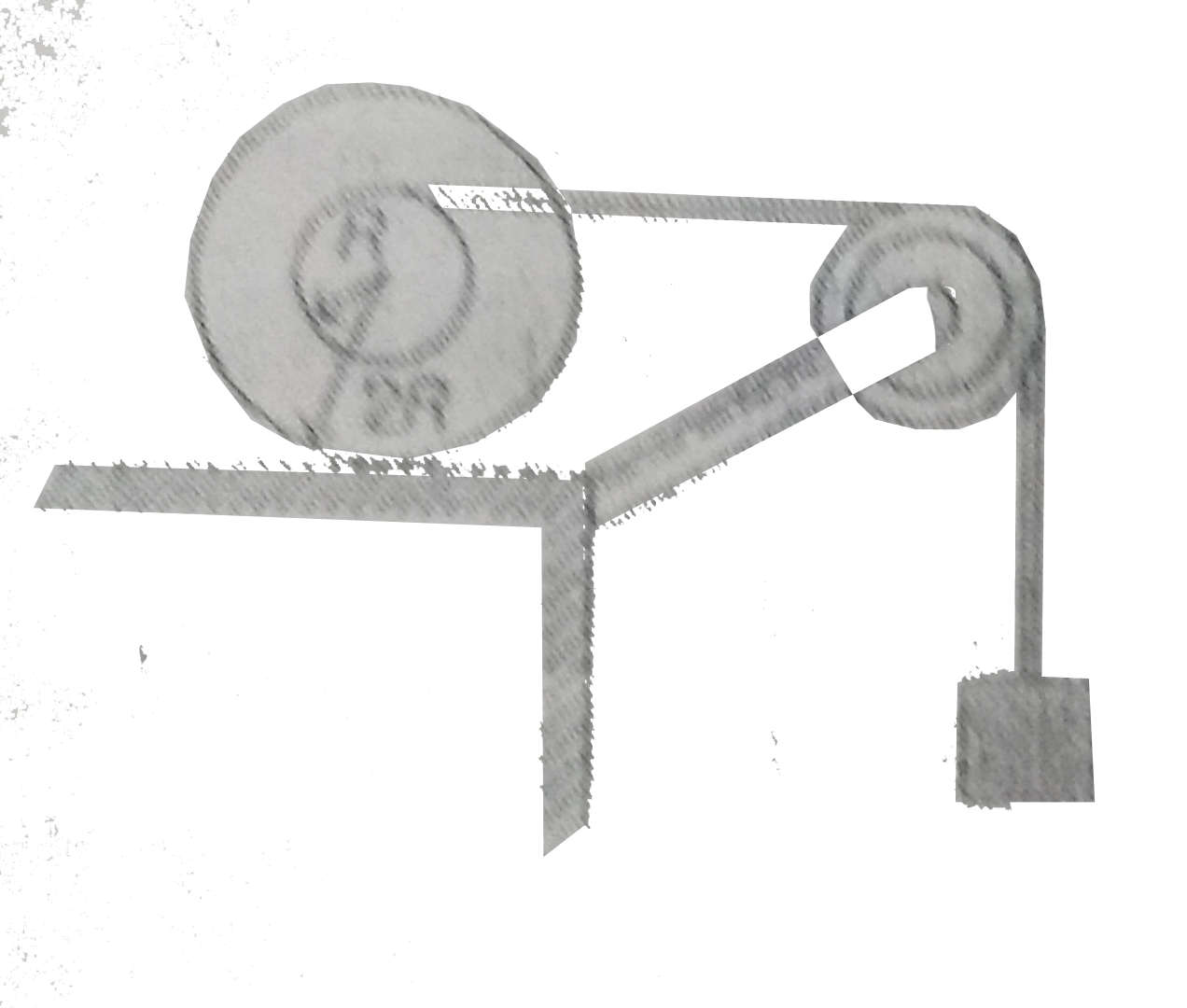 View Solution
View SolutionWhen a solid sphere rolls without slipping on a surface, its rotational kinetic energy is 40 J. Then its total kinetic energy is
View SolutionWhen a sphere rolls without slipping the ratio of its kinetic energy of translation to its total kinetic energy is.
View Solution

