In the above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then
t1=t2
t1<t2
t1>t2
None of these
The correct Answer is:B
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions41videos
ROTATIONAL MOTION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
Knowledge Check
- Question 1 - Select One
In above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then :
At1=t2Bt1<t2Ct1>t2DNone of these - Question 2 - Select One
Assertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is fasleDIf Assertion is false but Reason is true - Question 3 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μg
Assertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.View SolutionIf a solid and a hollow conducting sphere have same radius then
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
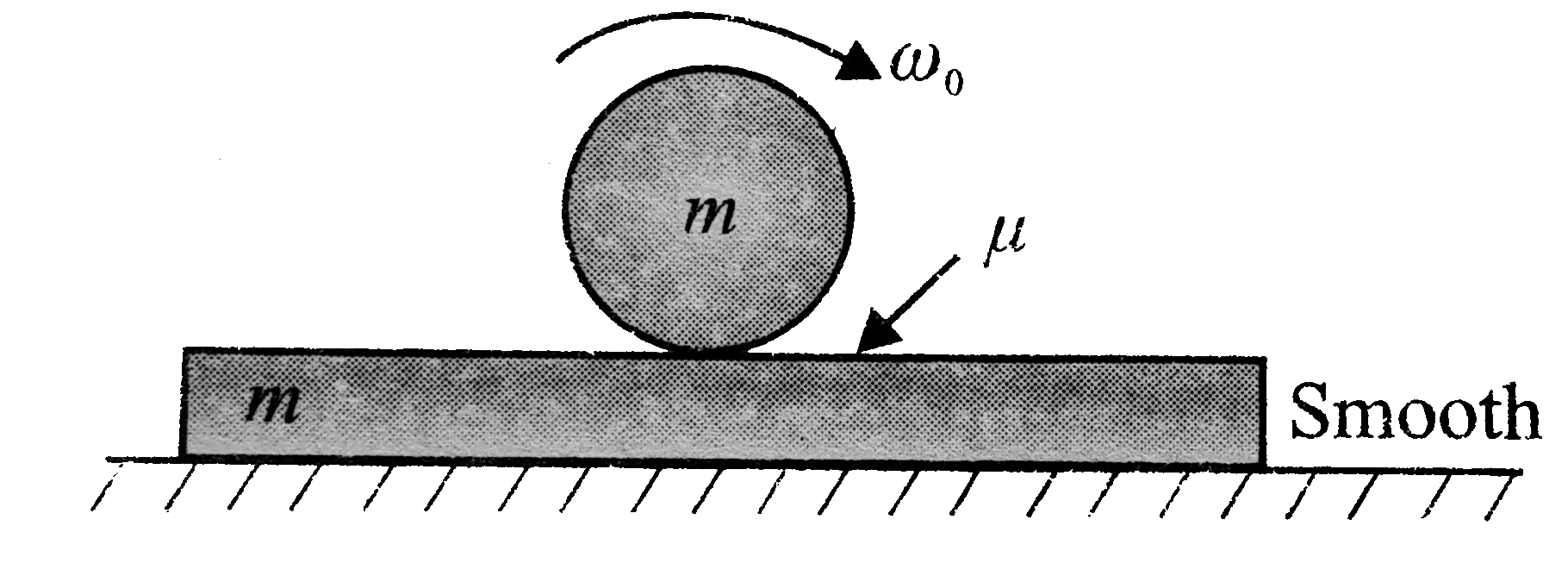
Find the velocity of the sphere after the pure rolling startsView SolutionIf a solid and a hollow conducting sphere have same radius then
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
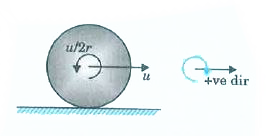
What will be the speed of sphere when it starts pure rolling?View Solution

