A uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes an angle $θ$ with horizontal. The cofficent of friction between the ring and plane is $μ$ . Initially, the point of contact of ring and plane is P. Angular momentum of ring about an axis passing from point P and perpendicular to plane of motion as a function of time t is

A

$m g R (sin θ) t - μ m g R (cos θ) t$

B

$m g R (sin θ) t$

C

$m g R (sin θ) t + μ m g R (cos θ) t$

D

$m g R (1 - μ^{2}) (sin θ) t$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$
Question 2 - Select One
A ring of mass $m$ and radius $R$ is rolling down on a rough inclined plane of angle $θ$ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
A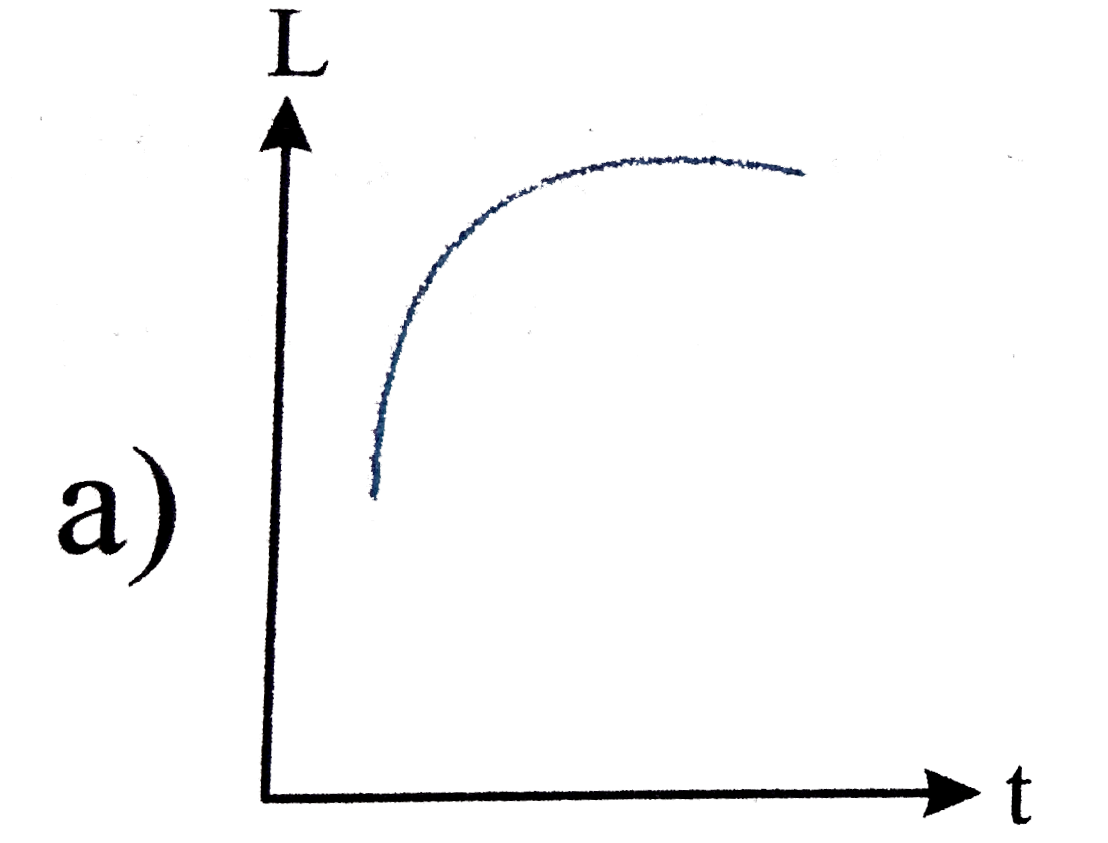
B
C
D
Question 3 - Select One
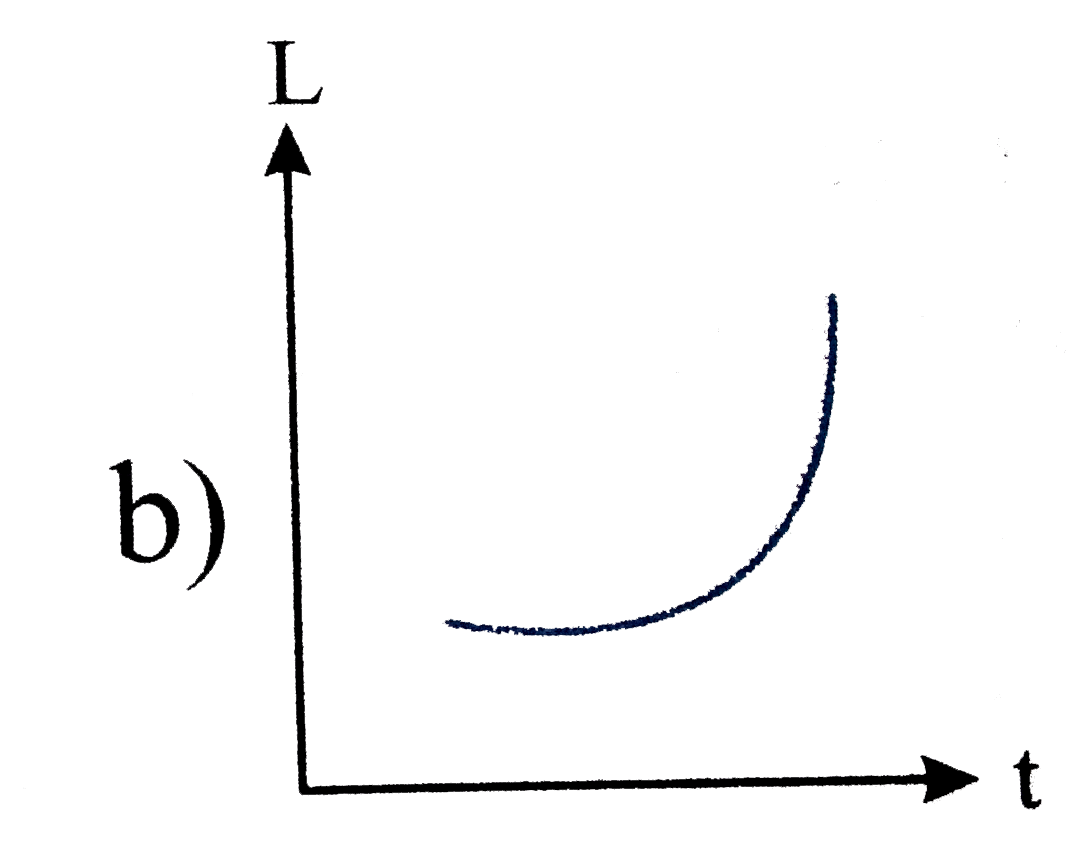Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is $4 k g m^{2}$ .
A $12 k g m^{2}$
B $3 k g m^{2}$
C $6 k g m^{2}$
D $9 k g m^{2}$

DC PANDEY-ROTATIONAL MOTION-A Only One Option is Correct

Home
Ask Doubt
Profile