A plank of mass M is placed over smooth inclined plane and sphere is also placed over the plank. Friction is sufficient between sphere and plank. If plank and sphere are released from rest, the frictional force on sphere is -
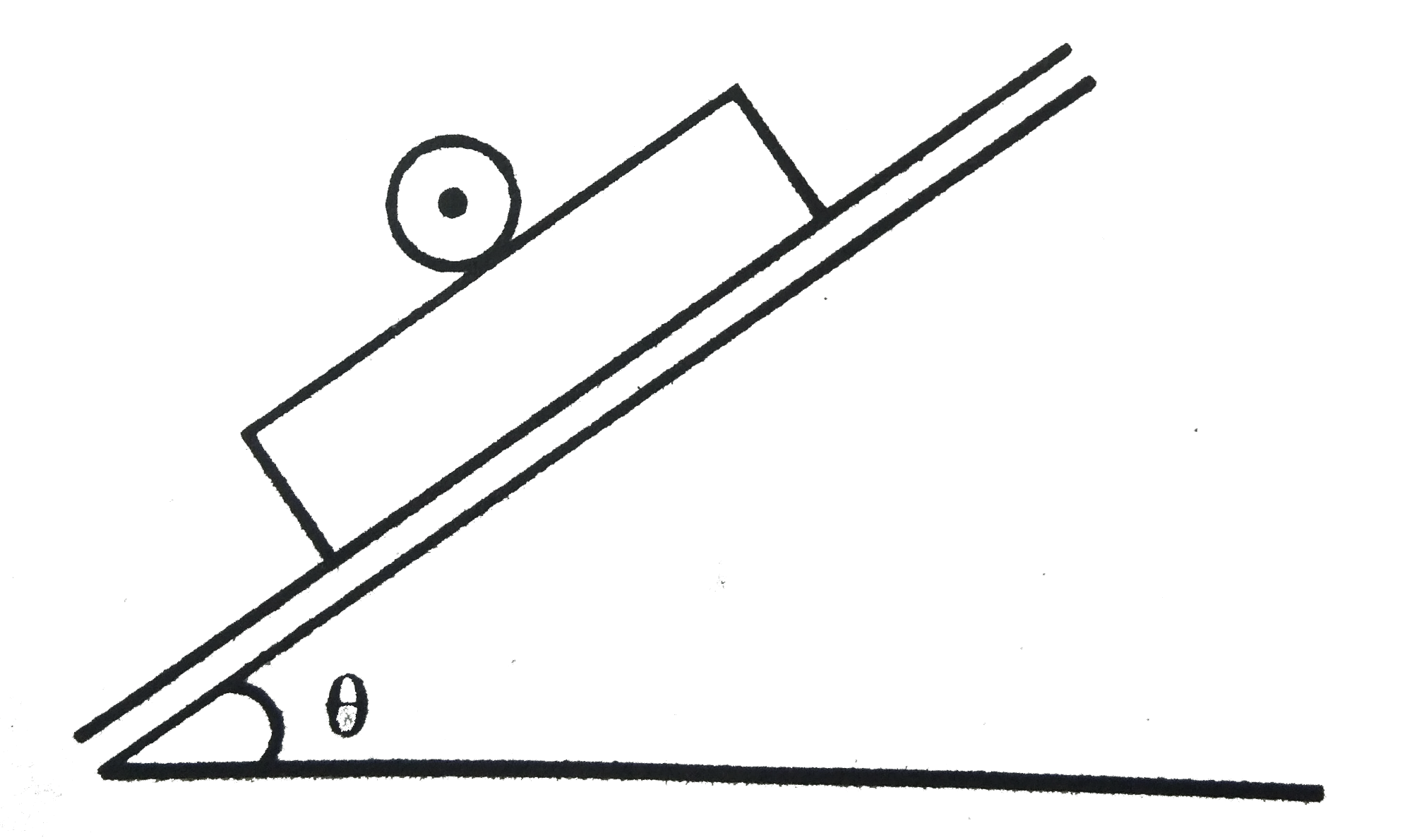 .
.
up the plane
down the plane
zero
maybe up or down the plane
The correct Answer is:C
Step by step video, text & image solution for A plank of mass M is placed over smooth inclined plane and sphere is also placed over the plank. Friction is sufficient between sphere and plank. If plank and sphere are released from rest, the frictional force on sphere is - . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
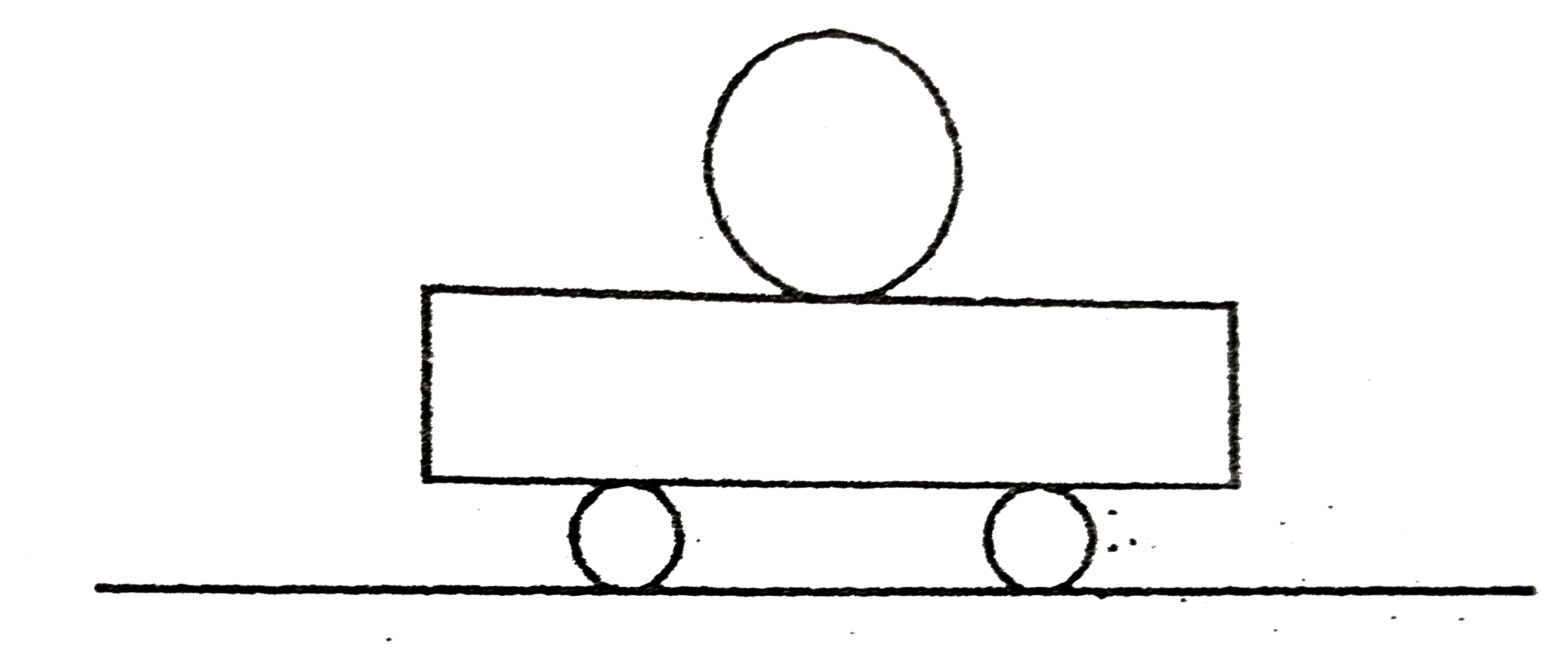
Angular acceleration of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View Solution
Knowledge Check
A plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of does not slide is:
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2A plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB2ω20r227μgC4ω20r281μgD2ω20r281μg
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
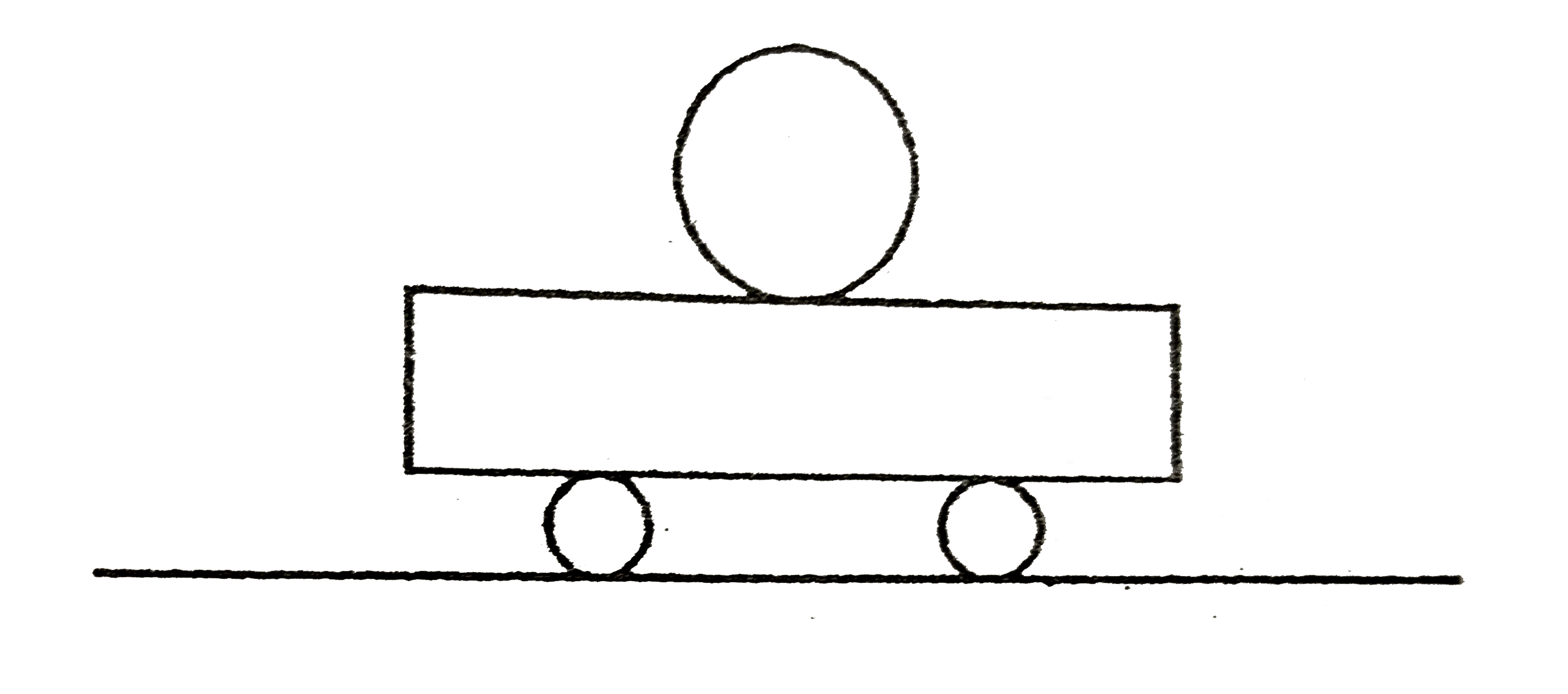
Acceleration of centre of mass of sphere is
View SolutionFind the acceleration of a system consisting of a cylinder of mass m and radius R and a plank of mass M placed an a smooth surface if it is pulled with a force F as shown Fig. Given that sufficient friction is present between the cylinder and the plank surface to prevent sliding of the cylinder.

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View Solution
