A plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
To solve the problem of finding the time after which the sphere begins pure rolling on the plank, we can follow these steps:
Step 1: Analyze the Forces Acting on the Sphere
When the plank is given a velocity v, the sphere experiences a frictional force F acting in the direction of the plank's motion. This frictional force is responsible for accelerating the sphere. The maximum static friction can be given by:
F=μmg
where μ is the coefficient of friction, m is the mass of the sphere, and g is the acceleration due to gravity.
Step 2: Determine the Acceleration of the Sphere
The frictional force causes the sphere to accelerate. According to Newton's second law:
F=ma⟹μmg=ma
Thus, the acceleration a of the sphere is:
a=μg
Step 3: Calculate the Velocity of the Sphere
The initial velocity of the sphere is 0. After a time t, the velocity vs of the sphere can be expressed as:
vs=0+at=μgt
Step 4: Analyze the Motion of the Plank
The frictional force also acts on the plank, causing it to decelerate. The acceleration of the plank ap is given by:
F=Map⟹μmg=Map⟹ap=μmgM
Since the plank is initially moving with velocity v, its velocity vp after time t is:
vp=v−apt=v−μmgMt
Step 5: Condition for Pure Rolling
For pure rolling to occur, the velocity of the sphere at its point of contact with the plank must equal the velocity of the plank at that point. The velocity of the point of contact on the sphere is given by:
vcontact=vs−rω
where ω is the angular velocity of the sphere. For pure rolling, we have:
vs−rω=vp
Step 6: Relate Angular Velocity to Linear Acceleration
The angular acceleration α of the sphere is related to its linear acceleration a by:
α=ar=μgr
Thus, the angular velocity ω after time t is:
ω=αt=μgrt
Step 7: Substitute and Solve for Time
Substituting vs, vp, and ω into the pure rolling condition:
μgt−r(μgrt)=v−μmgMt
This simplifies to:
μgt−μgt=v−μmgMt
Thus, we have:
0=v−(μmgM+μg)t
Rearranging gives:
t=vμmgM+μg
Step 8: Simplify the Expression
Factoring out μg:
t=vμg(mM+1)
Final Result
The time after which the sphere begins pure rolling is:
t=vμg(1+mM)
When the plank is given a velocity v, the sphere experiences a frictional force F acting in the direction of the plank's motion. This frictional force is responsible for accelerating the sphere. The maximum static friction can be given by:
F=μmg
where μ is the coefficient of friction, m is the mass of the sphere, and g is the acceleration due to gravity.
The frictional force causes the sphere to accelerate. According to Newton's second law:
F=ma⟹μmg=ma
Thus, the acceleration a of the sphere is:
a=μg
The initial velocity of the sphere is 0. After a time t, the velocity vs of the sphere can be expressed as:
vs=0+at=μgt
The frictional force also acts on the plank, causing it to decelerate. The acceleration of the plank ap is given by:
F=Map⟹μmg=Map⟹ap=μmgM
Since the plank is initially moving with velocity v, its velocity vp after time t is:
vp=v−apt=v−μmgMt
For pure rolling to occur, the velocity of the sphere at its point of contact with the plank must equal the velocity of the plank at that point. The velocity of the point of contact on the sphere is given by:
vcontact=vs−rω
where ω is the angular velocity of the sphere. For pure rolling, we have:
vs−rω=vp
The angular acceleration α of the sphere is related to its linear acceleration a by:
α=ar=μgr
Thus, the angular velocity ω after time t is:
ω=αt=μgrt
Substituting vs, vp, and ω into the pure rolling condition:
μgt−r(μgrt)=v−μmgMt
This simplifies to:
μgt−μgt=v−μmgMt
Thus, we have:
0=v−(μmgM+μg)t
Rearranging gives:
t=vμmgM+μg
Factoring out μg:
t=vμg(mM+1)
The time after which the sphere begins pure rolling is:
t=vμg(1+mM)
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)10videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)14videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type6videos
PHYSICS PART2
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
Similar Questions
A plank of mass M is moving on a smooth horizontal surface with speed 'v0'. At t=0 a sphere of mass 'm' and radius 'r' is gently placed on it and simultaneously a constant horizontal force 'F' is applied on the plank in the opposite direction of v0. Find the time at which sphere starts rolling on the plank. The coefficient of friction between the plank and the sphere is μ.
 View Solution
View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.View Solution
Knowledge Check
- Question 1 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB2ω20r227μgC4ω20r281μgD2ω20r281μg - Question 2 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling startsA2ω0r9Bω0r9Cω03D2ω0r3 - Question 3 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
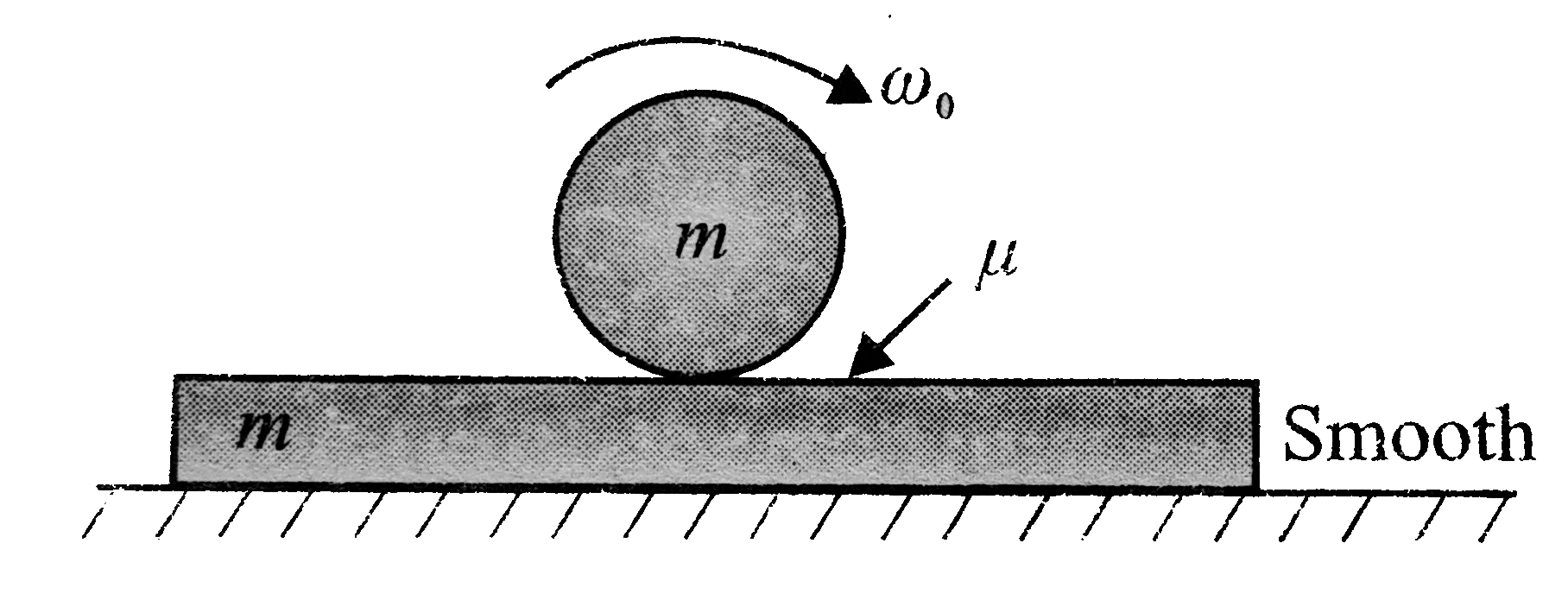
Find the time t at which the pure roiling startsAω0r9μgB2ω0r9μgCω0r3μgD2ω0rμg
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank
 View Solution
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?View SolutionA solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,
 View Solution
View SolutionA ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
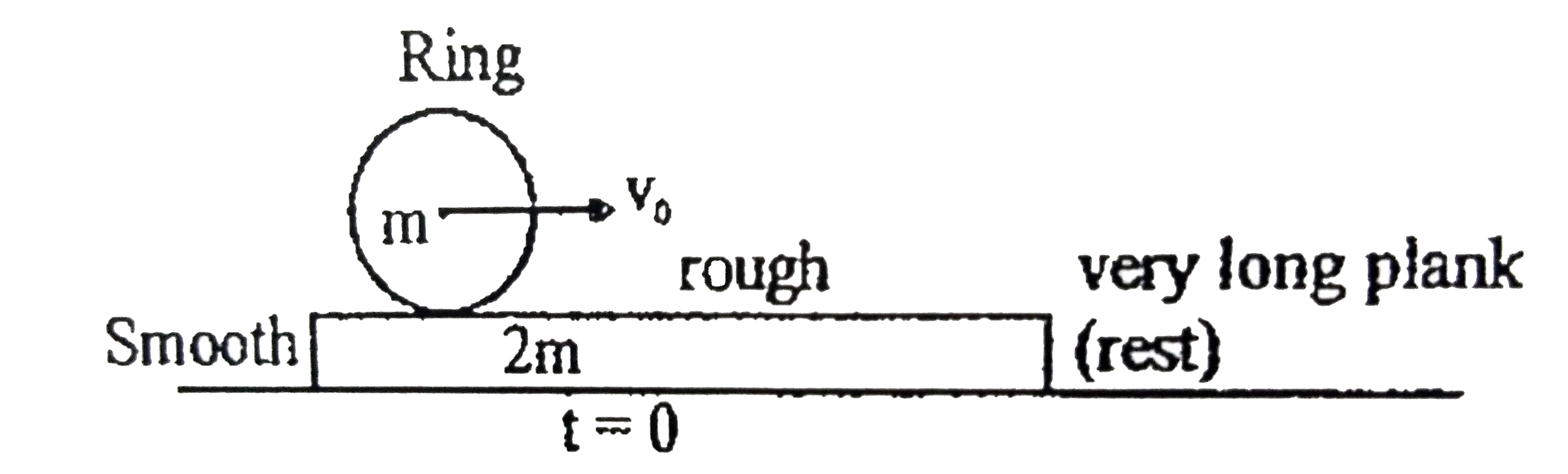 View Solution
View Solution

